深度学习基础

Uncategorized
3.1k words

前言

FYT视觉组培训，针对RoboMaster的深度学习速成课。

预备知识：

  • 学习完前面的C++培训知识，有基本的编程能力。
  • 掌握Python的基本语法。

参考书籍：

  • Deep Learning with Python Second Edition (主要讲tensorflow)
  • DIVE INTO DEEP LEARNING (主要讲pytorch)
  • 了解CV与RoboMaster视觉组 (视觉组圣经)

往年的深度学习文档：https://github.com/CSU-FYT-Vision/Vision-Tutorial

讲解人

计科2205 蔡明辰

1. 初识深度学习

1.1 什么是深度学习

深度学习（Deep Learning）是机器学习的一种方法，它利用多层神经网络对数据进行学习，并通过反向传播算法进行梯度下降，从而使得神经网络能够自动学习到数据的特征，并对未知数据进行预测。

1.2 RoboMaster与深度学习

在RoboMaster中，有许多需要使用到深度学习的地方，如图像识别、目标检测等。

  • 装甲板检测：可以使用实时目标检测装甲板的位置，准确有效击打装甲板。
  • 装甲数字识别：使用一个简单的图像分类网络，识别数字。
  • 雷达：目标检测赛场上的各种敌我车辆，显示小地图，发动易伤buff。

所以RMer视觉也要掌握深度学习的基本知识。

1.3 机器学习与深度学习

1.3.1 机器学习

机器学习的主要任务是从数据中学习，并利用这些知识对未知数据进行预测或决策。机器学习的算法有监督学习、无监督学习、半监督学习、强化学习等。

  • 输入数据。机器学习的输入数据可以是图像、文本、声音、视频等。
  • 预期输出示例。机器学习的预期输出可以是分类、回归、聚类、排序等。
  • 衡量算法效果的方法。衡量结果是一种反馈信号，用于调整算法。这个调整的步骤就是我们说的学习。

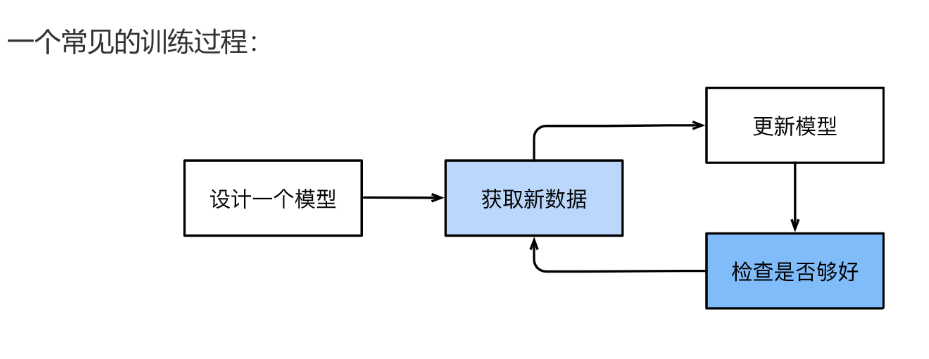
机器学习和深度学习的核心问题在于有意义地变换数据。换句话说，在于学习输入数据的有用表示——这种表示可以让数据更接近预期输出。

了解了学习的概念后，看看深度学习的特别之处。

1.3.2 深度学习之“深度”

深度学习是机器学习的一个分支，它利用多层神经网络对数据进行学习。

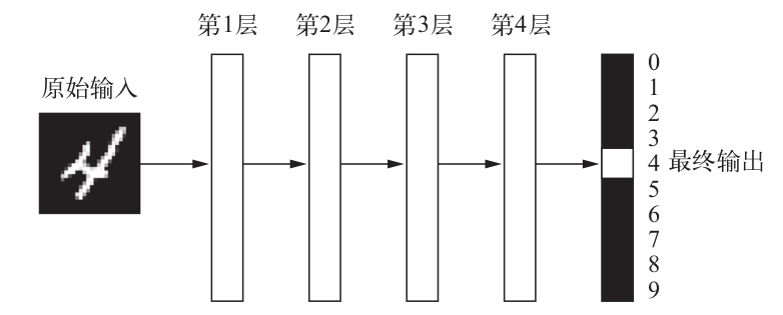
可以将深度神经网络看做一个多级的信息蒸馏：信息穿过多层过滤器，其纯度越来越高。

1.4 机器学习算法

本小节了解即可。

1.4.1 监督学习

监督学习擅长在“给定输入特征”的情况下预测标签。

监督学习的学习过程一般可以分为三大步骤：

  1. 从已知大量数据样本中随机选取一个子集，为每个样本获取真实标签。有时，这些样本已有标签（例如，患者是否在下一年内康复？）；有时，这些样本可能需要被人工标记（例如，图像分类）。这些输入和相应的标签一起构成了训练数据集；

  2. 选择有监督的学习算法，它将训练数据集作为输入，并输出一个“已完成学习的模型”；

  3. 将之前没有见过的样本特征放到这个“已完成学习的模型”中（测试集），使用模型的输出作为相应标签的预测。

  • 回归问题：输出是数值类型

    举例：通过各种影响因素预测房价、预测用户对一部电影的评分可以被归类为一个回归问题

  • 分类问题：输出是类别的分类问题的常见损失函数被称为 交叉熵 （cross-entropy）

    举例：从手写数据集中区分0~9（类别问题）、以下图片是否是毒蘑菇（二分类问题）

模型通常给出的是一个概率：比如输入以上蘑菇，分类器可能输出0.8
可以这样理解：分类器90%确定图像描绘的是一只猫

1.4.2 无监督学习

监督学习要向模型提供巨大数据集：每个样本包含特征和相应标签值。

相反，如果工作没有十分具体的目标，就需要“自发”地去学习了。 比如，老板可能会给我们一大堆数据，然后要求用它做一些数据科学研究，却没有对结果有要求。 这类数据中不含有“目标”的机器学习问题通常被为 无监督学习（unsupervised learning）

  • 聚类 （clustering）问题：没有标签的情况下，我们是否能给数据分类呢？比如，给定一组照片，我们能把它们分成风景照片、狗、婴儿、猫和山峰的照片吗？同样，给定一组用户的网页浏览记录，我们能否将具有相似行为的用户聚类呢？

  • 主成分分析 （principal component analysis）问题：我们能否找到少量的参数来准确地捕捉数据的线性相关属性？比如，一个球的运动轨迹可以用球的速度、直径和质量来描述。再比如，裁缝们已经开发出了一小部分参数，这些参数相当准确地描述了人体的形状，以适应衣服的需要。另一个例子：在欧几里得空间中是否存在一种（任意结构的）对象的表示，使其符号属性能够很好地匹配?这可以用来描述实体及其关系，例如“罗马” − “意大利” + “法国” = “巴黎”。

  • 因果关系 （causality）和 概率图模型 （probabilistic graphical models）问题：我们能否描述观察到的许多数据的根本原因？例如，如果我们有关于房价、污染、犯罪、地理位置、教育和工资的人口统计数据，我们能否简单地根据经验数据发现它们之间的关系？

  • 生成对抗性网络 （generative adversarial networks）：为我们提供一种合成数据的方法，甚至像图像和音频这样复杂的非结构化数据。潜在的统计机制是检查真实和虚假数据是否相同的测试，它是无监督学习的另一个重要而令人兴奋的领域。

1.4.3 半监督学习

半监督学习（Semi-Supervised Learning, SSL）是一种介于监督学习和无监督学习之间的机器学习方法。它利用少量标注数据和大量未标注数据共同训练模型，目标是提高模型的性能，同时减少对标注数据的依赖。半监督学习方法在标注数据获取成本较高或数据标注较困难的场景中非常有用，例如医学影像分析、自然语言处理和计算机视觉等领域。

  • 标记样本少的类别：可以用聚类算法来标记样本少的类别。
  • 标记样本多的类别：可以用生成模型来标记样本多的类别。

1.4.4 强化学习

强化学习（Reinforcement Learning）是机器学习的一种方法，它通过与环境的互动来学习。

强化学习的目标是产生一个好的 策略 （policy）。

模型根据对环境的观察产生一定的动作，将这个动作应用到环境当中，模型从环境中获得 奖励

举例：AlphaGo

本科毕设 非嵌入式离线强化学习制作皇室战争AI与8000分人机的获胜对局

1.4 用三张图理解深度学习的工作原理

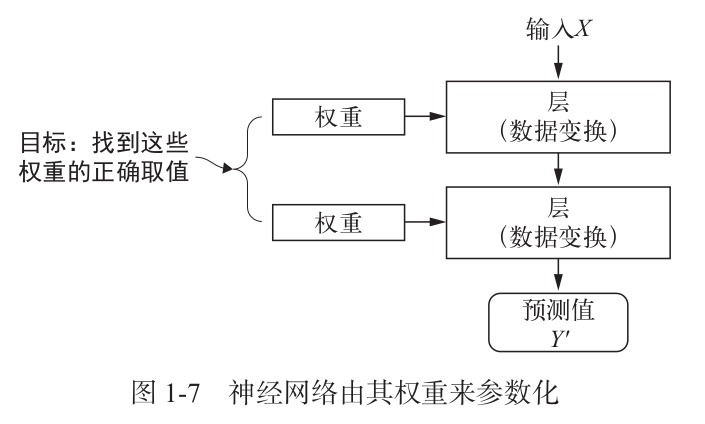
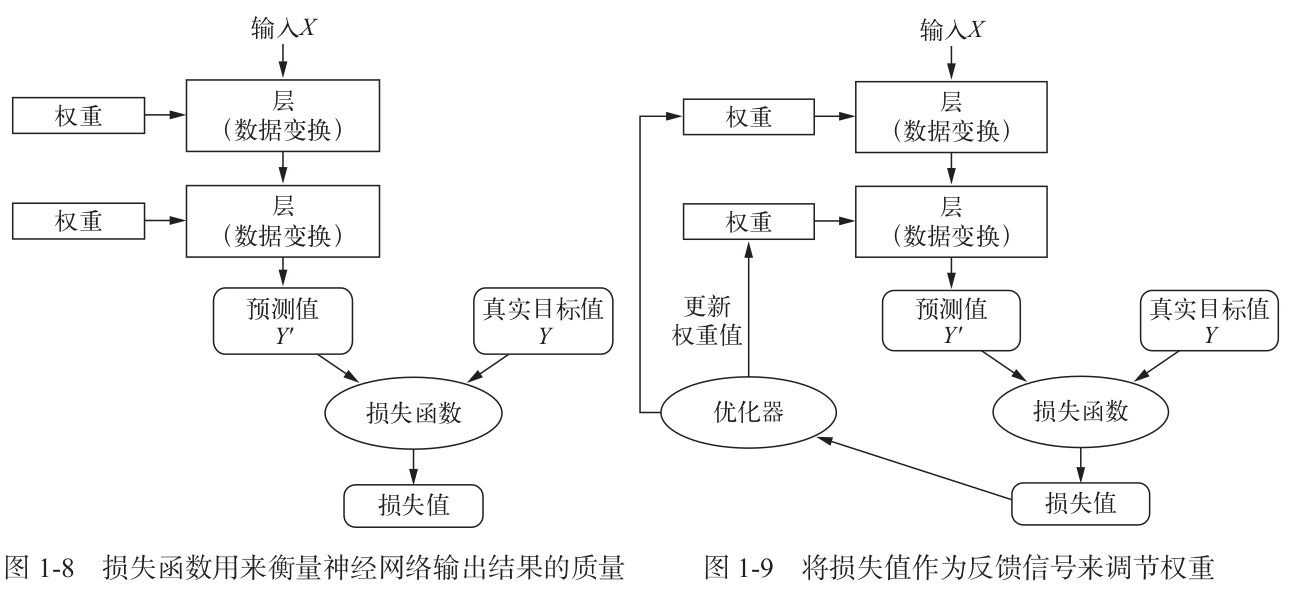
1.5 深度学习的硬件

CPU、GPU、TPU(张量处理器)

【硬核科普】从零开始认识显卡

2007年，NVIDIA推出了CUDA，它是一种基于GPU的并行编程模型，可以让程序员编写并行代码，并在GPU上运行。

1.6 深度学习的历史与发展

1.6.1 神经网络的核心关键原则：

  1. 线性和非线性处理单元的交替
    通常称为层（layers）。
  2. 使用链式规则（也称为反向传播 Backpropagation）
    一次性调整网络中的全部参数。

1.6.2深度学习的提出历史：

  • 一些中流砥柱的模型：
    • 多层感知机（McCulloch and Pitts, 1943）
    • 卷积神经网络（LeCun et al., 1998）
    • 长短期记忆网络（Graves and Schmidhuber, 2005）
    • Q学习（Watkins and Dayan, 1992）
  • 曾因对休眠期和当时技术限制被搁置一段时间后，过去十年被重新发现。

1.6.3 为什么最近十几年深度学习才重新“热门”？

  1. 网络和图像传感器的发展使得数据的获取变得廉价
    • 大量图片、视频和用户数据信息使得大规模数据集变得触手可及。
  2. 运算设备的算力发展
    • GPU的普及，使大规模算力唾手可得。
  3. 深度学习框架在传播想法方面发挥了至关重要的作用
    • 例如，PyTorch 和 TensorFlow。
    • 在2014年之前，对卡内基梅隆大学机器学习博士生来说，训练全性能回归模型曾是一个复杂的作业问题。而现在，这项任务只需不到10行代码即可完成。

2. 神经网络的基本数学概念

2.1 张量 (Tensor) 介绍

张量是多维数组的泛化，用于表示标量、向量、矩阵及更高维数据。

  1. 标量 (Scalar)
    标量是零维张量，仅表示一个数值，例如： 

    1
    x = np.array(5)  # 标量

  2. 向量 (Vector)
    向量是一维张量，例如： 

    1
    x = np.array([1, 2, 3])  # 向量

  3. 矩阵 (Matrix)
    矩阵是二维张量，例如： 

    1
    x = np.array([[1, 2], [3, 4]])  # 矩阵

  4. 张量 (Tensor)
    张量是更高维度的数组

2.2 张量运算的导数——梯度 (Gradient)

导数这一概念可以应用于任意函数，只要函数所对应的表面是连续且光滑的。张量运算（或张量函数）的导数叫作梯度（gradient）。梯度就是将导数这一概念推广到以张量为输入的函数，张量函数的梯度表示该函数所对应多维表面的曲率（curvature）。

2.3 随机梯度下降 (Stochastic Gradient Descent)

给定一个可微函数，理论上可以用解析法找到它的最小值，但在实际中，求解析解往往是不可行的。

一个两个参数求解析解还好说，但是神经网络的参数不会少于几千个，而且经常有上千万个。

SGD的步骤：

  1. 抽取训练样本 x 和对应目标 y_true 组成的一个数据批量。
  2. 在 x 上运行模型，得到预测值 y_pred。这一步叫作前向传播。
  3. 计算模型在这批数据上的损失值，用于衡量 y_pred 和 y_true 之间的差距。
  4. 计算损失相对于模型参数的梯度。这一步叫作反向传播（backward pass）。
  5. 将参数沿着梯度的反方向移动一小步，比如 W -= learning_rate* gradient，从而使这批数据上的损失值减小一些。学习率（learning_rate）是一个调节梯度下降“速度”的标量因子。

一维损失函数曲线的随机梯度下降
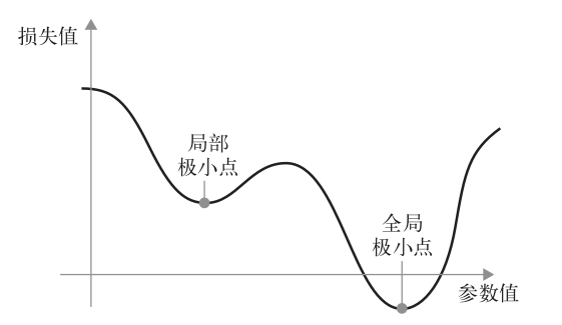
如你所见，直观上来看，learning_rate 因子的取值很重要。如果取值太小，那么沿着曲线下降需要很多次迭代，而且可能会陷入局部极小点。如果取值过大，那么更新权重值之后可能会出现在曲线上完全随机的位置。

2.5 优化器 (Optimizer)

优化器是用于最小化损失函数的算法，通过梯度更新神经网络的参数。

常见优化器

  1. 随机梯度下降 (SGD)
  • 批量随机梯度下降，随机梯度下降，小批量随机梯度下降
  1. AdaGrad
  • 适合处理稀疏数据，但学习率可能逐渐变小。
  1. RMSProp
  • 通过均方根调整学习率，适合非平稳目标。
  1. Adam
    综合了动量法和 RMSProp：

2.2 链式求导（Chain Rule）

链式求导是神经网络梯度计算的核心工具，用于计算复合函数的导数。

如果函数 $z = f(g(x))$，则导数计算为：

$$
\frac{\partial z}{\partial x} = \frac{\partial z}{\partial g} \cdot \frac{\partial g}{\partial x}
$$

在神经网络中，每一层的输出是上一层的输入，链式求导用于将输出误差逐层反传以更新权重。

2.4 反向�