自学小白的卡尔曼滤波实例

前记

你有没有在看卡尔曼滤波方程式感到非常烧脑，对一堆高斯分布等数学推理感到困惑?反正我是这样。如果你和我一样只想知道如何运用卡尔曼滤波完成一些例子，学会如何使用卡尔曼滤波做控制的话，希望本文可以为你提供一点帮助。

一、卡尔曼滤波(KF)拟合y=sin(x)曲线

假设我们要使用卡尔曼滤波对带有噪声的 sin(x) 数据进行拟合，并输出拟合曲线的图像，同时预测 x=7.5 时的 sin(x) 值。

1. 先贴一个代码

   import numpy as np
   import matplotlib.pyplot as plt
   
   # 系统模型参数
   dt = 0.05  # 时间步长（采样点更加密集）
   A = np.array([[1]])  # 状态转移矩阵
   B = np.array([[0]])  # 控制矩阵（无控制输入）
   C = np.array([[1]])  # 观测矩阵
   Q = np.array([[1e-4]])  # 过程噪声协方差
   R = np.array([[0.1]])  # 观测噪声协方差
   P = np.array([[1]])  # 初始估计误差协方差
   x0 = np.array([[0]])  # 初始状态
   
   # 生成带噪声的sin(x)数据
   np.random.seed(42)  # 固定随机种子，保证结果可重复
   x_vals = np.arange(0, 7.05, dt)  # 采样点从 0 到 7
   true_vals = np.sin(x_vals)  # sin(x) 的真实值
   noise = np.random.normal(0, np.sqrt(R[0][0]), size=true_vals.shape)  # 生成噪声
   observed_vals = true_vals + noise  # 带噪声的观测值
   
   # 初始状态
   x_est = x0
   P_est = P
   
   # 存储预测结果
   estimates = []
   
   # 卡尔曼滤波过程
   for z in observed_vals:
       # 预测
       x_pred = A @ x_est  # 状态预测
       P_pred = A @ P_est @ A.T + Q  # 误差协方差预测
   
       # 更新
       z = np.array([[z]])  # 当前的观测值
       y = z - C @ x_pred  # 观测残差
       S = C @ P_pred @ C.T + R  # 残差协方差
       K = P_pred @ C.T @ np.linalg.inv(S)  # 卡尔曼增益
   
       x_est = x_pred + K @ y  # 状态更新
       P_est = (np.eye(len(P)) - K @ C) @ P_pred  # 误差协方差更新
   
       estimates.append(x_est[0][0])  # 存储估计值
   
   # 在最后一次更新后，进行未来预测
   # 预测 x=7.5 的状态
   x_future = x_est  # 以最后的估计作为基础
   for _ in range(1, int(7.5 / dt) - len(observed_vals) + 1):
       x_future = A @ x_future  # 状态转移预测
   
   # 预测的 y 值
   y_future_pred = x_future[0][0]
   
   # 转换为numpy数组
   estimates = np.array(estimates)
   
   # 绘制带噪声的观测值、真实值以及卡尔曼滤波的拟合结果
   plt.figure(figsize=(10, 6))
   plt.plot(x_vals, observed_vals, 'r.', label="Noisy observations", markersize=4)
   plt.plot(x_vals, true_vals, 'b-', label="True sin(x)")
   plt.plot(x_vals, estimates, 'g-', label="Kalman filter estimate")
   
   # 在图中标出 x=7.5 的预测值
   plt.scatter([7.5], [y_future_pred], color='purple', label=f"Predicted y at x=7.5: {y_future_pred:.2f}", zorder=5)
   plt.axvline(x=7.5, color='purple', linestyle='--', alpha=0.6)
   
   # 标题和图例
   plt.legend()
   plt.xlabel("x")
   plt.ylabel("y")
   plt.title("Kalman Filter Fitting to Noisy sin(x) Data with Prediction at x=7.5")
   plt.grid(True)
   plt.xlim(0, 7.5)  # 设置x轴范围
   plt.ylim(-1.5, 1.5)  # 设置y轴范围
   plt.show()
   
   # 打印预测的 x=7.5 时的 y 值
   print(f"预测 x=7.5 时的 y 值: {y_future_pred:.2f}")

2. 了解参数矩阵

这些系统模型参数是在卡尔曼滤波中定义系统的动态模型和噪声特性的核心部分。每个参数都有特定的含义和作用，下面详细解释这些参数：

1. dt = 1.0（时间步长）

• 解释：表示系统的时间步长。尽管在这个例子中没有直接使用 dt，但它在很多动态系统中非常重要，尤其是当系统随时间变化时，dt 用来表示离散时间步之间的间隔。
• 作用：如果状态随时间演化，比如位置、速度等，时间步长可以影响状态的更新方式。在这个简单的例子中，状态（y 值）直接随 x 的增量变化。

2. A = np.array([[1]])（状态转移矩阵）

• 解释：状态转移矩阵 ( A ) 定义了系统的当前状态如何转移到下一个状态。在这里 A 是一个 1x1 的矩阵，值为 1，表示状态在时间步之间没有变化。
• 作用：在卡尔曼滤波中，状态更新公式为：
  [
  x_{k+1} = A \cdot x_k + B \cdot u_k
  ]
  在这里，A = 1 表示状态 x 没有因时间推移而改变（保持不变）。

3. B = np.array([[0]])（控制矩阵）

• 解释：控制矩阵 ( B ) 用于将控制输入 ( u_k ) 转换为对系统状态的影响。在这个例子中，B 是一个 1x1 的矩阵，值为 0，表示系统没有外部控制输入。
• 作用：如果系统有控制输入（比如机器人上的电机控制信号），那么 B 就会将输入影响到系统状态中。在这个例子中，因为我们不考虑控制输入，B = 0，所以外部输入对系统没有影响。

4. C = np.array([[1]])（观测矩阵）

• 解释：观测矩阵 ( C ) 定义了系统的状态如何映射到观测值。C = 1 表示我们直接观测系统的状态，没有任何变换。
• 作用：在卡尔曼滤波的观测更新中，观测模型如下：
  [
  z_k = C \cdot x_k + v_k
  ]
  其中 ( z_k ) 是观测值，C 定义了如何从状态 ( x_k ) 得到观测值。在这里，C = 1，表示观测值就是系统的真实状态。

5. Q = np.array([[1e-5]])（过程噪声协方差）

• 解释：过程噪声协方差 ( Q ) 表示系统内部状态转移过程中的不确定性或噪声。这里设置的 ( Q = 1e-5 )，表示状态演化过程中的噪声较小。
• 作用：这描述了系统的动态模型中的随机扰动。当系统不确定性较高时，可以将 ( Q ) 设置得更大。较大的 ( Q ) 值意味着你相信系统模型中的噪声更大，预测不够准确，观测更新将更重要。

6. R = np.array([[1e-2]])（观测噪声协方差）

• 解释：观测噪声协方差 ( R ) 定义了观测到的数据中所包含的噪声程度。这里设置的 ( R = 1e-2 )，表示观测值中有一定的噪声。
• 作用：较大的 ( R ) 值意味着你认为观测数据较不可靠，滤波器在更新状态时会更多依赖状态预测，而不是观测值。较小的 ( R ) 值表示你对观测值更有信心。

7. P = np.array([[1]])（初始估计误差协方差）

• 解释：初始估计误差协方差 ( P ) 描述了初始状态的不确定性。这里设置的 ( P = 1 )，表示我们对初始状态的置信度一般，不确定性较大。
• 作用：卡尔曼滤波器的每一步都会更新这个估计误差协方差矩阵，用来衡量当前状态的不确定性。初始的较大 ( P ) 表示对初始状态的估计不太精确，但随着滤波过程，滤波器会逐步降低不确定性。

8. x0 = np.array([[1]])（初始状态）

• 解释：初始状态 ( x0 ) 是我们开始卡尔曼滤波时的假设系统状态。在这里，设置为 1，表示在 ( x = 0 ) 时，初始状态 ( y(0) = 1 )。
• 作用：这是滤波的起点，随着新的观测和预测，卡尔曼滤波器将逐渐修正这一初始状态，使其逼近真实状态。

这些参数定义了卡尔曼滤波器在估计和预测状态时所需要的系统模型：

• 状态转移矩阵 ( A ) 和 观测矩阵 ( C ) 定义了状态如何随时间变化，以及如何观测到状态。
• 噪声协方差 ( Q ) 和 ( R ) 定义了过程中的随机性或不确定性。
• 初始状态 ( x0 ) 和 初始估计误差协方差 ( P ) 定义了卡尔曼滤波的起点，以及对初始状态的不确定性。

你可以根据系统的特性和数据的噪声程度调整这些参数，以获得更精确的估计和预测。

3. 运行并调整参数矩阵

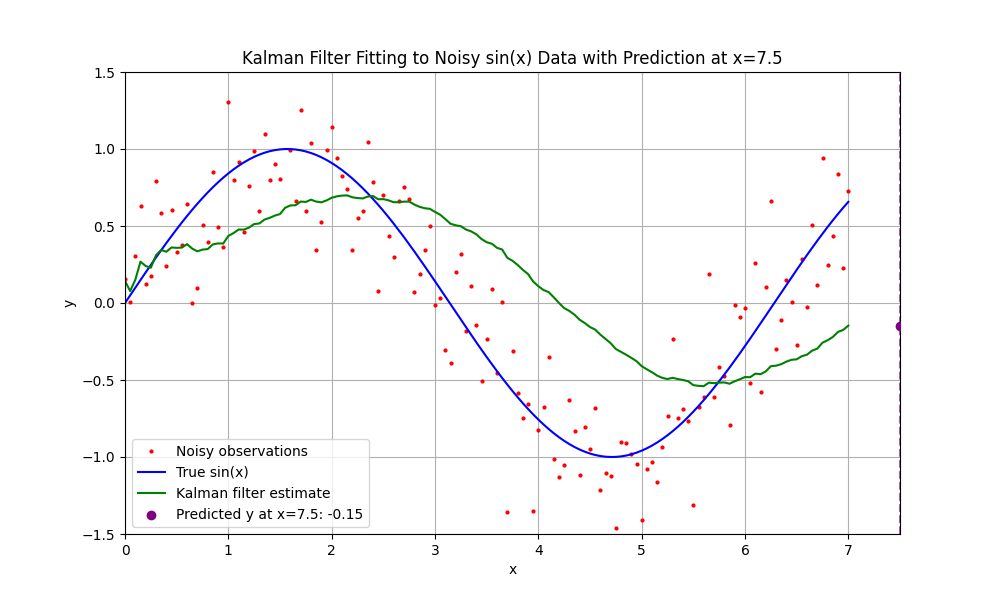
发现是这样的，卡尔曼滤波的曲线好像并没有很好的拟合住 sin(x)，这时我们就要调整上面说的 Q 矩阵(过程噪声矩阵)，将它的值调大，以更好的拟合 sin(x)，但是这样会卡尔曼滤波曲线抖动会更加剧烈。

将 Q 调为 1e-3 后发现拟合还差点，调为 1e-1 发现确实差不多在 sin(x) 上下，但是抖动剧烈，调为 1e-2 就差不多了

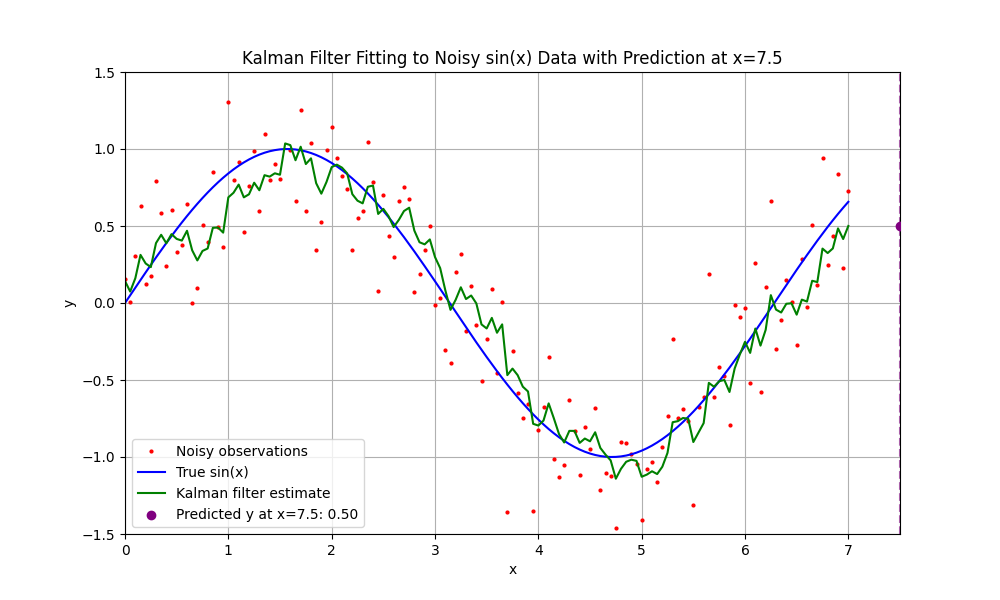
但是，有个问题就是预测的 x=7.5 的值会和 x=7 的值是一模一样的，因为状态矩阵是 [1] ，就是状态不变。所以要用到别的线性状态矩阵了。

1. 线性状态转移

   A = np.array([[1]])  # 当前状态不变

2. 一阶差分（增加预测能力）

   A = np.array([[1, dt], [0, 1]])  # 状态转移矩阵，包含位置和速度

3. 二次状态转移（更复杂的模型）

   A = np.array([[1, dt, 0.5 * dt**2], 
             [0, 1, dt], 
             [0, 0, 1]])  # 增加加速度状态

这里我们先用一次状态转移

import numpy as np
import matplotlib.pyplot as plt

# 系统模型参数
dt = 0.05  # 时间步长（采样点更加密集）
A = np.array([[1, dt],   # 状态转移矩阵，位置和速度
              [0, 1]])  # 位置和速度
B = np.array([[0], 
              [0]])  # 控制矩阵（无控制输入）
C = np.array([[1, 0]])  # 观测矩阵，只观测位置
Q = np.array([[1e-2, 0],  # 过程噪声协方差
              [0, 1e-2]])

R = np.array([[0.05]])  # 观测噪声协方差

P = np.array([[1, 0], 
              [0, 1]])  # 初始估计误差协方差
x0 = np.array([[0], 
                [0]])  # 初始状态（位置为0，速度为0）

# 生成带噪声的sin(x)数据
np.random.seed(42)  # 固定随机种子，保证结果可重复
x_vals = np.arange(0, 7.05, dt)  # 采样点从 0 到 7
true_vals = np.sin(x_vals)  # sin(x) 的真实值
noise = np.random.normal(0, np.sqrt(R[0][0]), size=true_vals.shape)  # 生成噪声
observed_vals = true_vals + noise  # 带噪声的观测值

# 初始状态
x_est = x0
P_est = P

# 存储预测结果
estimates = []

# 卡尔曼滤波过程
for z in observed_vals:
    # 预测
    x_pred = A @ x_est  # 状态预测
    P_pred = A @ P_est @ A.T + Q  # 误差协方差预测

    # 更新
    z = np.array([[z]])  # 当前的观测值
    y = z - C @ x_pred  # 观测残差
    S = C @ P_pred @ C.T + R  # 残差协方差
    K = P_pred @ C.T @ np.linalg.inv(S)  # 卡尔曼增益

    x_est = x_pred + K @ y  # 状态更新
    P_est = (np.eye(len(P)) - K @ C) @ P_pred  # 误差协方差更新

    estimates.append(x_est[0][0])  # 存储估计值

# 在最后一次更新后，进行未来预测
# 预测 x=7.5, 8, 8.5, 9, 9.5, 10 的状态
future_x_values = np.arange(7.5, 10.5, 0.5)  # 未来的x值
future_predictions = []

for x_future in future_x_values:
    # 基于当前的状态进行预测
    for _ in range(int((x_future - x_vals[-1]) / dt)):
        x_est = A @ x_est  # 状态转移预测
    future_predictions.append(x_est[0][0])  # 存储预测的y值

# 转换为numpy数组
estimates = np.array(estimates)
future_predictions = np.array(future_predictions)

# 绘制带噪声的观测值、真实值以及卡尔曼滤波的拟合结果
plt.figure(figsize=(10, 6))
plt.plot(x_vals, observed_vals, 'r.', label="Noisy observations", markersize=4)
plt.plot(x_vals, true_vals, 'b-', label="True sin(x)")
plt.plot(x_vals, estimates, 'g-', label="Kalman filter estimate")

# 在图中标出未来预测的值
for future_x, future_y in zip(future_x_values, future_predictions):
    plt.scatter([future_x], [future_y], color='purple', label=f"Predicted y at x={future_x:.1f}: {future_y:.2f}", zorder=5)
    plt.axvline(x=future_x, color='purple', linestyle='--', alpha=0.6)

# 标题和图例
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.title("Kalman Filter Fitting to Noisy sin(x) Data with Predictions")
plt.grid(True)
plt.xlim(0, 10)  # 设置x轴范围
plt.ylim(-1.5, 5)  # 设置y轴范围
plt.show()

# 打印预测的 y 值
for future_x, future_y in zip(future_x_values, future_predictions):
    print(f"预测 x={future_x:.1f} 时的 y 值: {future_y:.2f}")

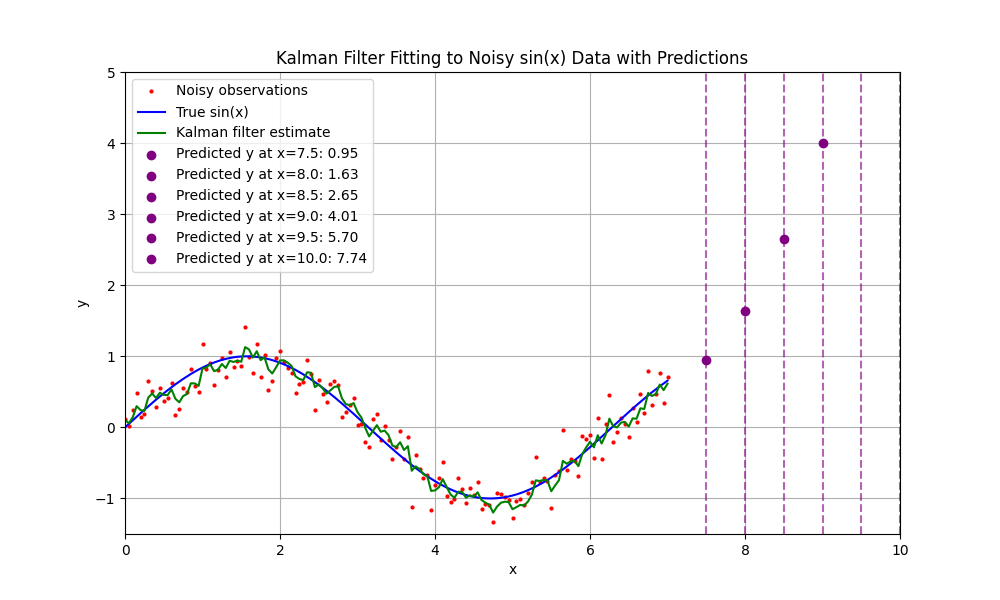
发现后面的点可以预测了。

二、扩展卡尔曼滤波(EKF)

扩展卡尔曼滤波（Extended Kalman Filter, EKF）是一种高效处理非线性系统的状态估计算法。它通过线性化非线性模型来近似系统动态和观测模型，从而允许使用卡尔曼滤波的框架。

import numpy as np
import matplotlib.pyplot as plt

# 状态转移函数：x[0] 是位置，x[1] 是速度
def f(x, u, dt):
    """
    非线性状态转移函数，基于正弦函数动态。
    x[0] = 当前的x值
    x[1] = 当前的速度
    """
    return np.array([x[0] + x[1]*dt, x[1]])  # 假设状态为 [x, dx/dt]

# 观测函数：观测的是 sin(x[0])
def h(x):
    """
    非线性观测模型，基于 y = sin(x)。
    """
    return np.array([np.sin(x[0])])

# 状态转移方程的雅可比矩阵
def jacobian_f(x, u, dt):
    """
    f 的雅可比矩阵，线性化状态转移方程。
    """
    return np.array([[1, dt], [0, 1]])

# 观测方程的雅可比矩阵
def jacobian_h(x):
    """
    h 的雅可比矩阵，线性化观测方程。
    """
    return np.array([[np.cos(x[0]), 0]])

# 初始化参数
x_est = np.array([0, 1])  # 初始状态估计 [x, dx/dt]
P = np.array([[1, 0], 
              [0, 1]])  # 初始状态协方差矩阵
Q = np.array([[0.01, 0], 
              [0, 0.01]])  # 过程噪声协方差
R = np.array([[0.1]])  # 观测噪声协方差
dt = 0.05  # 时间步长
u = 0  # 没有外部控制输入

# 用于存储结果
true_x = np.linspace(0, 10, 100)  # 真实 x (0到10)
true_y = np.sin(true_x)  # 真实的 y = sin(x)
noisy_observations = true_y + np.random.normal(0, 0.1, size=true_y.shape)  # 带噪声的观测

# 预测和估计
x_ekf_estimates = []
for z in noisy_observations:
    # 预测步骤
    F = jacobian_f(x_est, u, dt)
    x_pred = f(x_est, u, dt)
    P_pred = F @ P @ F.T + Q
    
    # 更新步骤
    H = jacobian_h(x_pred)
    y = z - h(x_pred)  # 观测残差
    S = H @ P_pred @ H.T + R  # 残差协方差
    K = P_pred @ H.T @ np.linalg.inv(S)  # 卡尔曼增益
    x_est = x_pred + K @ y  # 更新状态估计
    P = (np.eye(2) - K @ H) @ P_pred  # 更新协方差矩阵

    x_ekf_estimates.append(h(x_est)[0])  # 存储估计的 sin(x) 值

# 扩展预测：x = 11, 12, 13
future_x = np.array([11, 12, 13])
future_y_estimates = []

for x_val in future_x:
    F = jacobian_f(x_est, u, dt)
    x_pred = f(x_est, u, dt)  # 预测下一步
    x_est = x_pred  # 更新状态估计为当前预测值
    future_y_estimates.append(h(x_est)[0])  # 预测的 sin(x) 值

# 将真实值和EKF估计值进行比较
plt.plot(true_x, true_y, label='True sin(x)', color='blue')
plt.scatter(true_x, noisy_observations, label='Noisy observations', color='red', s=10)
plt.plot(true_x, x_ekf_estimates, label='EKF estimate', color='green')
plt.scatter(future_x, future_y_estimates, label='Predicted x = 11,12,13', color='orange', s=50)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('EKF Fitting to Noisy sin(x) Data with Future Predictions')
plt.show()

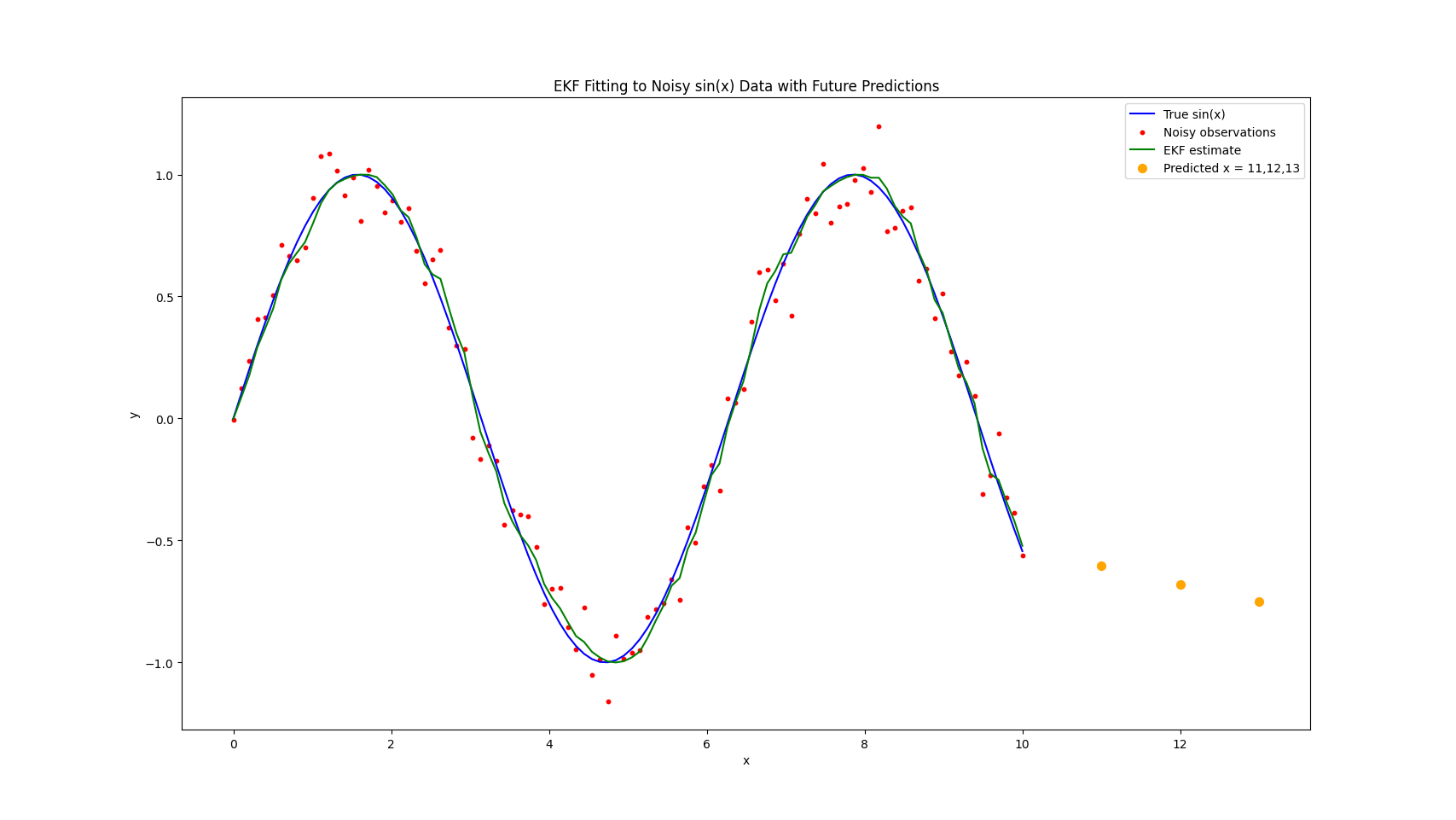
发现拟合和预测都变得好了很多很多。

扩展卡尔曼滤波器（EKF）是一种用于非线性系统状态估计的算法。它通过对系统的状态转移方程和观测方程进行线性化处理，使得卡尔曼滤波能够应用于非线性问题。EKF广泛应用于机器人定位、导航、目标跟踪等领域，可以在带有噪声的环境中，结合传感器数据，实时估计系统的状态，如位置、速度等。

下面一篇文章将正式运用EKF完成一个识别+跟踪的项目(^-^)。