【算法实验】解题实验报告

2024-06-29

Uncategorized

5.2k words

计科2205班蔡明辰

实验一

本实验主要是分治算法

T1 快速排序及第k小数

问题描述

实现快速排序算法，并利用快速排序算法的思想解决第k小数的问题。

解题思路

快速排序：快速排序是一种分治算法，通过选择一个”枢轴”元素，将数组分成左右两个部分，左边部分的元素都小于或等于枢轴，右边部分的元素都大于或等于枢轴，然后递归地对左右两部分进行排序。
第k小数：可以利用快速排序的思想，通过每次划分数组，确定第k小数所在的位置，如果这个位置恰好是k，那么找到了第k小数；如果位置小于k，则第k小数在右边部分；如果位置大于k，则第k小数在左边部分。

完整代码

快速排序

#include <iostream>
#include <vector>

void quickSort(std::vector<int>& arr, int left, int right) {
    if (left < right) {
        int pivotIndex = partition(arr, left, right);
        quickSort(arr, left, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, right);
    }
}

int partition(std::vector<int>& arr, int left, int right) {
    int pivot = arr[right];
    int i = left - 1;
    for (int j = left; j < right; ++j) {
        if (arr[j] <= pivot) {
            ++i;
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[right]);
    return i + 1;
}

void printArray(const std::vector<int>& arr) {
    for (int i = 0; i < arr.size(); ++i) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
}

int main() {
    std::vector<int> arr = {10, 7, 8, 9, 1, 5};
    int n = arr.size();
    quickSort(arr, 0, n - 1);
    std::cout << "Sorted array: ";
    printArray(arr);
    return 0;
}

第k小数

#include <iostream>
#include <vector>

int partition(std::vector<int>& arr, int left, int right) {
    int pivot = arr[right];
    int i = left - 1;
    for (int j = left; j < right; ++j) {
        if (arr[j] <= pivot) {
            ++i;
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[right]);
    return i + 1;
}

int quickSelect(std::vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];
    }
    int pivotIndex = partition(arr, left, right);
    if (k == pivotIndex) {
        return arr[k];
    } else if (k < pivotIndex) {
        return quickSelect(arr, left, pivotIndex - 1, k);
    } else {
        return quickSelect(arr, pivotIndex + 1, right, k);
    }
}

int main() {
    std::vector<int> arr = {10, 4, 5, 8, 6, 11, 26};
    int n = arr.size();
    int k = 3;
    std::cout << "The " << k << "rd smallest element is " << quickSelect(arr, 0, n - 1, k - 1) << std::endl;
    return 0;
}

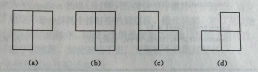
T2 棋盘覆盖问题

问题描述

在一个 $2^k \times 2^k $ 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖

解题思路

分治法：将大棋盘划分为4个子棋盘，每个子棋盘的大小为 $2^{k-1} \times 2^{k-1}$。
放置L型骨牌：确定4个子棋盘中的哪个包含特殊方格，然后在另外3个子棋盘的交汇处放置一个L型骨牌，使得这3个子棋盘各自有一个新的特殊方格。
递归覆盖：递归处理每个子棋盘，直到子棋盘的大小为 $2 \times 2$ 时，直接用一个L型骨牌覆盖。

完整代码

#include <iostream>
#include <vector>

const int MAXN = 1024;  // 最大棋盘大小
int board[MAXN][MAXN];  // 棋盘
int tile = 1;           // L型骨牌标记

// 覆盖函数
void coverBoard(int tr, int tc, int dr, int dc, int size) {
    if (size == 1) return;

    int t = tile++;  // 当前L型骨牌标记
    int s = size / 2;

    // 覆盖左上角子棋盘
    if (dr < tr + s && dc < tc + s) {
        coverBoard(tr, tc, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s - 1] = t;
        coverBoard(tr, tc, tr + s - 1, tc + s - 1, s);
    }

    // 覆盖右上角子棋盘
    if (dr < tr + s && dc >= tc + s) {
        coverBoard(tr, tc + s, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s] = t;
        coverBoard(tr, tc + s, tr + s - 1, tc + s, s);
    }

    // 覆盖左下角子棋盘
    if (dr >= tr + s && dc < tc + s) {
        coverBoard(tr + s, tc, dr, dc, s);
    } else {
        board[tr + s][tc + s - 1] = t;
        coverBoard(tr + s, tc, tr + s, tc + s - 1, s);
    }

    // 覆盖右下角子棋盘
    if (dr >= tr + s && dc >= tc + s) {
        coverBoard(tr + s, tc + s, dr, dc, s);
    } else {
        board[tr + s][tc + s] = t;
        coverBoard(tr + s, tc + s, tr + s, tc + s, s);
    }
}

// 打印棋盘
void printBoard(int size) {
    for (int i = 0; i < size; ++i) {
        for (int j = 0; j < size; ++j) {
            std::cout << board[i][j] << "\t";
        }
        std::cout << std::endl;
    }
}

int main() {
    int k = 3;  // 棋盘大小2^k
    int n = 1 << k;
    int dr = 1, dc = 2;  // 特殊方格位置

    coverBoard(0, 0, dr, dc, n);
    printBoard(n);

    return 0;
}

测试结果

3  3  4  4  8  8  9  9
3  2  0  4  8  7  7  9
5  2  2  6  10 10 7  11
5  5  6  6  1  10 11 11
13 13 14 1  1  18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21

其中的数字0就代表特殊方格，没有填入骨牌。

实验三

本实验主要考察的是动态规划

T1 计算矩阵连乘积

问题描述

这个问题是经典的矩阵链乘问题，目的是找到一种最优的计算顺序，使得计算矩阵连乘的总次数最少。下面是对程序的详细解释和修改后的代码，确保可以正确计算最小的数乘次数。

解题思路

问题定义：给定n个矩阵，要求找到计算矩阵连乘积的最优顺序，使得计算的数乘次数最少。
递归公式：
- 设 $ m[i][j] $ 表示计算从矩阵 $ A_i $ 到 $ A_j $ 的最小数乘次数。
- 设 $ p $ 是矩阵的维数数组，表示矩阵 $ A_i $ 的维数为 $ p[i-1] \times p[i] $。
- 初始条件： m[i][i] = 0 。
- 递归公式：
  $$
  m[i][j] = \min_{i \leq k < j} { m[i][k] + m[k+1][j] + p[i-1] \times p[k] \times p[j] }
  $$
实现步骤：
- 读入矩阵的维数数组 p 。
- 初始化 m[i][i] = 0 。
- 使用递归公式计算 m[i][j] 。

完整代码

#include <stdio.h>

int main() {
    int p[101], i, j, k, r, t, n;
    int m[101][101]; // m[i][j]表示计算从矩阵Ai到Aj的最小数乘次数
    int s[101][101]; // 记录从第i到第j个矩阵连乘的断开位置

    // 读入矩阵的数量
    scanf("%d", &n);
    for (i = 0; i <= n; i++) {
        scanf("%d", &p[i]); // 读入矩阵的维数数组
    }

    // 初始化m[i][i]=0，即单个矩阵的连乘次数为0
    for (i = 1; i <= n; i++) {
        m[i][i] = 0;
    }

    // 递归计算矩阵连乘的最小数乘次数
    for (r = 1; r < n; r++) { // r为i、j相差的值
        for (i = 1; i <= n - r; i++) { // i为行
            j = i + r; // j为列
            m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j]; // 给m[i][j]赋初值
            s[i][j] = i; // 记录断开位置
            for (k = i + 1; k < j; k++) {
                t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (t < m[i][j]) {
                    m[i][j] = t; // m[i][j]取最小值
                    s[i][j] = k; // 记录断开位置
                }
            }
        }
    }

    // 输出最小的数乘次数
    printf("%d\n", m[1][n]);

    return 0;
}

T2 防卫导弹

问题描述

一种新型的防卫导弹可截击多个攻击导弹。它可以向前飞行，也可以用很快的速度向下飞行，可以毫无损伤地截击进攻导弹，但不可以向后或向上飞行。但有一个缺点，尽管它发射时可以达到任意高度，但它只能截击比它上次截击导弹时所处高度低或者高度相同的导弹。现对这种新型防卫导弹进行测试，在每一次测试中，发射一系列的测试导弹（这些导弹发射的间隔时间固定，飞行速度相同），该防卫导弹所能获得的信息包括各进攻导弹的高度，以及它们发射次序。现要求编一程序，求在每次测试中，该防卫导弹最多能截击的进攻导弹数量，一个导弹能被截击应满足下列两个条件之一：

它是该次测试中第一个被防卫导弹截击的导弹；
它是在上一次被截击导弹的发射后发射，且高度不大于上一次被截击导弹的高度的导弹。

输入数据：第一行是一个整数n，以后的n各有一个整数表示导弹的高度。

输出数据：截击导弹的最大数目。

分析：定义l[i]为选择截击第i个导弹，从这个导弹开始最多能截击的导弹数目。

由于选择了第i枚导弹，所以下一个要截击的导弹j的高度要小于等于它的高度，所以l[i]应该等于从i＋1到n的每一个j，满足h[j]<=h[i]的j中l[j]的最大值。

这个问题可以通过动态规划来解决。目标是找出最长的非递增子序列（Longest Non-Increasing Subsequence, LNIS），即最多可以截击的导弹数量。以下是对程序的解释以及代码：

解题思路

定义状态：
- 设 $ l[i] $ 为选择截击第 $ i $ 个导弹后，从这个导弹开始最多能截击的导弹数目。
状态转移方程：
- 如果选择截击第 $ i $ 个导弹，那么下一个要截击的导弹 $ j $ 的高度必须小于等于第 $ i $ 个导弹的高度。所以：
  $$
  l[i] = \max_{i < j \leq n} { l[j] } + 1 \quad \text{其中} \quad h[j] \leq h[i]
  $$
初始化：
- 最后一个导弹只能截击自己，所以 $ l[n-1] = 1 $。
结果：
- 输出 $ l[0] $，即从第一个导弹开始最多能截击的导弹数目。

完整代码

#include <stdio.h>

int main() {
    int i, j, n, max, h[100], l[100];
    
    // 读入导弹数量
    scanf("%d", &n);
    
    // 读入各个导弹的高度
    for (i = 0; i < n; i++)
        scanf("%d", &h[i]);
    
    // 初始化最后一个导弹的截击数目
    l[n - 1] = 1;
    
    // 逆向遍历导弹
    for (i = n - 2; i >= 0; i--) {
        max = 0;
        for (j = i + 1; j < n; j++)
            if (h[i] >= h[j] && max < l[j])
                max = l[j];
        l[i] = max + 1;
    }
    
    // 输出从第一个导弹开始最多能截击的导弹数目
    max = 0;
    for (i = 0; i < n; i++)
        if (l[i] > max)
            max = l[i];
    
    printf("%d\n", max);
    
    return 0;
}

T3 皇宫看守

问题描述

太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；某些宫殿间可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

请你编程计算帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

输入数据：输入数据由文件名为intput.txt的文本文件提供。输入文件中数据表示一棵树，描述如下：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号i(0<i<=n)，在该宫殿安置侍卫所需的经费k，该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，…，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出数据：输出到output.txt文件中。输出文件仅包含一个数，为所求的最少的经费。

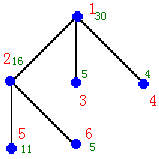
如右图的输入数据示例：

Sample Input

6 
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

Sample Output

解题思路

我们可以使用动态规划来求解此问题。定义 dp[i][0] 表示以节点 i 为根节点的子树中，不在节点 i 上安排侍卫的最小花费；dp[i][1] 表示以节点 i 为根节点的子树中，在节点 i 上安排侍卫的最小花费。

具体步骤如下：

初始化每个节点的费用和子节点信息。
使用深度优先搜索（DFS）遍历整棵树，并在遍历过程中计算每个节点的 dp 值。
根节点的两个 dp 值中的较小值即为所需的最小费用。

完整代码

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>

using namespace std;

const int MAXN = 1505;
int cost[MAXN];  // 保存每个节点的费用
int dp[MAXN][2]; // dp[i][0]表示不在节点i上安排侍卫的最小费用，dp[i][1]表示在节点i上安排侍卫的最小费用
vector<int> tree[MAXN]; // 存储树的结构

void dfs(int u) {
    dp[u][0] = 0; // 不在节点u上安排侍卫的最小费用初始化为0
    dp[u][1] = cost[u]; // 在节点u上安排侍卫的最小费用初始化为节点u的费用

    for (int v : tree[u]) {
        dfs(v); // 深度优先搜索遍历子节点v
        dp[u][0] += dp[v][1]; // 若不在u节点安排侍卫，则子节点必须安排侍卫
        dp[u][1] += min(dp[v][0], dp[v][1]); // 若在u节点安排侍卫，子节点可安排或不安排侍卫，取最小值
    }
}

int main() {
    freopen("input.txt", "r", stdin);
    freopen("output.txt", "w", stdout);

    int n;
    cin >> n;

    memset(cost, 0, sizeof(cost));
    memset(dp, 0, sizeof(dp));

    for (int i = 1; i <= n; ++i) {
        int id, k, m;
        cin >> id >> k >> m;
        cost[id] = k;
        for (int j = 0; j < m; ++j) {
            int child;
            cin >> child;
            tree[id].push_back(child);
        }
    }

    dfs(1); // 假设节点1为根节点进行dfs

    cout << min(dp[1][0], dp[1][1]) << endl;

    return 0;
}

测试结果

6 
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出结果为：

实验五

本实验主要是贪心算法和随机算法

T1 背包问题

问题描述

有一个背包，背包容量是M=150。有7个物品，物品可以分割成任意大小。

要求尽可能让装入背包中的物品总价值最大，但不能超过总容量。

物品	A	B	C	D	E	F	G
重量	35	30	60	50	40	10	25
价值	10	40	30	50	35	40	30

解题思路

计算每个物品的单位重量价值（价值/重量）。
按照单位重量价值从大到小排序物品。
依次选择物品装入背包，直到背包达到最大容量M。

完整代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 定义物品结构体
struct Item {
    double weight;
    double value;
    double unitValue; // 单位重量价值
};

// 比较函数，用于按单位重量价值从大到小排序
bool compare(Item a, Item b) {
    return a.unitValue > b.unitValue;
}

int main() {
    // 背包容量
    const double M = 150.0;
    
    // 物品信息
    vector<Item> items = {
        {35, 10},
        {30, 40},
        {60, 30},
        {50, 50},
        {40, 35},
        {10, 40},
        {25, 30}
    };
    
    // 计算每个物品的单位重量价值
    for (auto &item : items) {
        item.unitValue = item.value / item.weight;
    }
    
    // 按单位重量价值从大到小排序
    sort(items.begin(), items.end(), compare);
    
    double totalValue = 0.0; // 背包中物品的总价值
    double currentWeight = 0.0; // 背包当前重量
    
    for (auto &item : items) {
        if (currentWeight + item.weight <= M) {
            // 如果当前物品能完全装入背包
            currentWeight += item.weight;
            totalValue += item.value;
        } else {
            // 如果当前物品不能完全装入背包，装入部分
            double remainWeight = M - currentWeight;
            totalValue += item.unitValue * remainWeight;
            break;
        }
    }
    
    cout << "背包中物品的最大总价值: " << totalValue << endl;
    
    return 0;
}

T2 照亮的山景

问题描述

在一片山的上空，高度为T处有N个处于不同位置的灯泡，如图。如果山的边界上某一点于某灯i的连线不经过山的其它点，我们称灯i可以照亮该点。开尽量少的灯，使得整个山景都被照亮。山被表示成有m个转折点的折线。

提示：照亮整个山景相当于照亮每一个转折点。

解题思路

这个问题类似于一个覆盖问题，目标是使用尽量少的灯泡照亮整个山景。我们可以通过几何方法来解决这个问题。

输入处理：读取山的转折点和灯泡的位置。
可见性判断：判断每个灯泡是否能够照亮每个转折点。
集合覆盖问题：使用贪心算法解决最小集合覆盖问题，即选择尽量少的灯泡照亮所有转折点。

完整代码

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

struct Point {
    double x, y;
};

// 计算叉积
double crossProduct(Point a, Point b, Point c) {
    return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}

// 判断p1到p2的直线是否与山的折线相交
bool isVisible(Point p1, Point p2, vector<Point>& mountain) {
    for (size_t i = 0; i < mountain.size() - 1; ++i) {
        if (crossProduct(p1, mountain[i], p2) * crossProduct(p1, mountain[i + 1], p2) < 0 &&
            crossProduct(mountain[i], p1, mountain[i + 1]) * crossProduct(mountain[i], p2, mountain[i + 1]) < 0) {
            return false;
        }
    }
    return true;
}

int main() {
    int T, N, M;
    cin >> T >> N >> M;

    vector<Point> bulbs(N);
    for (int i = 0; i < N; ++i) {
        cin >> bulbs[i].x >> bulbs[i].y;
    }

    vector<Point> mountain(M);
    for (int i = 0; i < M; ++i) {
        cin >> mountain[i].x >> mountain[i].y;
    }

    vector<vector<int>> visibility(N, vector<int>(M, 0));

    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < M; ++j) {
            if (isVisible(bulbs[i], mountain[j], mountain)) {
                visibility[i][j] = 1;
            }
        }
    }

    vector<int> covered(M, 0);
    int minBulbs = 0;

    while (true) {
        int maxCover = 0, bestBulb = -1;
        for (int i = 0; i < N; ++i) {
            int cover = 0;
            for (int j = 0; j < M; ++j) {
                if (!covered[j] && visibility[i][j]) {
                    cover++;
                }
            }
            if (cover > maxCover) {
                maxCover = cover;
                bestBulb = i;
            }
        }
        
        if (maxCover == 0) break;

        minBulbs++;
        for (int j = 0; j < M; ++j) {
            if (visibility[bestBulb][j]) {
                covered[j] = 1;
            }
        }
    }

    cout << "最少需要的灯泡数量: " << minBulbs << endl;

    return 0;
}

代码说明

输入处理：读取灯泡和山的转折点坐标。
可见性判断：利用叉积判断两点连线是否经过山的其他点。
集合覆盖：使用贪心算法选择最少的灯泡，确保照亮所有转折点。

测试结果

假设我们有以下输入：

运行该程序会输出最少需要的灯泡数量。通过这种方法，我们可以确保以最少的灯泡照亮整个山景。

T3 搬桌子问题

问题描述

某教学大楼一层有n个教室，从左到右依次编号为1、2、…、n。现在要把一些课桌从某些教室搬到另外一些教室，每张桌子都是从编号较小的教室搬到编号较大的教室，每一趟，都是从左到右走，搬完一张课桌后，可以继续从当前位置或往右走搬另一张桌子。输入数据：先输入n、m，然后紧接着m行输入这m张要搬课桌的起始教室和目标教室。

输出数据：最少需要跑几趟。

解题思路

这个问题可以转化为寻找最少的区间覆盖问题。每次搬运一张桌子，可以理解为从一个区间的起始点到结束点的操作。因此，我们需要找到一种方法，能够用最少的区间数覆盖所有搬运任务。

一个有效的解法是使用贪心算法，步骤如下：

将所有搬运任务按照起始教室和目标教室进行排序。
使用一个变量跟踪当前的搬运终点位置，初始化为0。
遍历所有搬运任务，对于每一个任务，如果其起始教室在当前搬运终点位置之前，则可以在当前趟次中继续搬运。
否则，增加新的趟次，并更新当前搬运终点位置。

完整代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 任务结构体
struct Task {
    int start;
    int end;
};

// 比较函数，用于按起点和终点排序
bool compare(Task a, Task b) {
    if (a.start == b.start) {
        return a.end < b.end;
    }
    return a.start < b.start;
}

int main() {
    int n, m;
    cin >> n >> m;

    vector<Task> tasks(m);
    for (int i = 0; i < m; ++i) {
        cin >> tasks[i].start >> tasks[i].end;
    }

    // 按起始教室和目标教室排序
    sort(tasks.begin(), tasks.end(), compare);

    int trips = 0;
    int currentEnd = 0;

    for (int i = 0; i < m; ++i) {
        if (tasks[i].start > currentEnd) {
            // 如果当前任务的起始教室在当前搬运终点之后，需要新的趟次
            trips++;
            currentEnd = tasks[i].end;
        } else {
            // 如果当前任务的起始教室在当前搬运终点之前，可以继续搬运，更新终点
            currentEnd = max(currentEnd, tasks[i].end);
        }
    }

    cout << "最少需要跑 " << trips << " 趟" << endl;

    return 0;
}

代码解释

输入处理：读取教室的数量n和任务的数量m，然后读取每个任务的起始教室和目标教室。
任务排序：按照起始教室和目标教室对任务进行排序。
贪心算法：遍历所有任务，根据当前搬运的终点位置决定是否需要新的趟次，更新当前搬运终点位置。
输出结果：输出最少需要的跑趟数。

这样，我们就可以用最少的趟次完成所有搬运任务。

Tags

Archives

Recent Posts

实验一

T1 快速排序及第k小数

问题描述

解题思路

完整代码

快速排序

第k小数

T2 棋盘覆盖问题

问题描述

解题思路

完整代码

测试结果

实验三

T1 计算矩阵连乘积

问题描述

解题思路

完整代码

T2 防卫导弹

问题描述

解题思路

完整代码

T3 皇宫看守

问题描述

解题思路

完整代码

测试结果

实验五

T1 背包问题

问题描述

解题思路

完整代码

T2 照亮的山景

问题描述

解题思路

完整代码

代码说明

测试结果

T3 搬桌子问题

问题描述

解题思路

完整代码

代码解释