【算法题解】部分洛谷题解(上)

Uncategorized
9.5k words

前言

本篇为我做过的洛谷题的部分题解，大多是我认为比较具有代表性的或者比较有意思的题目，包含我自己的思考过程和想法。

[NOIP2001 提高组] 数的划分

题目描述

将整数 $n$ 分成 $k$ 份，且每份不能为空，任意两个方案不相同（不考虑顺序）。

例如：$n=7$，$k=3$，下面三种分法被认为是相同的。

$1,1,5$;
$1,5,1$;
$5,1,1$.

问有多少种不同的分法。

输入格式

$n,k$ （$6<n \le 200$，$2 \le k \le 6$）

输出格式

$1$ 个整数，即不同的分法。

样例 #1

样例输入 #1

1
7 3

样例输出 #1

1
4

提示

四种分法为：
$1,1,5$;
$1,2,4$;
$1,3,3$;
$2,2,3$.

【题目来源】

NOIP 2001 提高组第二题

解题思路

其是这题我一看下去觉得纯纯搜索就完了，就直接采用了DFS的思路，考虑一下递归边界，做一个可行性减枝，一顿搜索后就是60分。更换思路，改成从n-k+1到1循环，从后往前遍历i，觉得能够减少循环，把大的数字先找出来，是80分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<cstdio>
using namespace std;
int ans=0,n,k;
void dfs(int sum,int begin,int num){
	if(sum>n || num >k) return;
	if(sum==n && k==num){
		ans++;
		return;
	}
	//for(int i=begin;i<=n-1;i++) //60分，未优化
	for(int i=begin;i>=1;i--)     //80分 
		dfs(sum+i,i,num+1);		
}
int main(){
	scanf("%d%d",&n,&k);
	dfs(0,n-k+1,0);
	printf("%d",ans);
	return 0;
}

仔细思考后，发现原来是边界条件搞错了。。。

修改后就是100分了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<cstdio>
using namespace std;
int ans=0,n,k;
void dfs(int sum,int begin,int num){
	if(sum>n || num >k) return;
	if(k==num){
		if(sum==n)
			ans++;
		return;
	}
	for(int i=begin;i>=1;i--)
		dfs(sum+i,i,num+1); 
}
int main(){
	scanf("%d%d",&n,&k);
	//dfs(0,1,0);
	dfs(0,n-k+1,0);
	printf("%d",ans);
	return 0;
}

其实这道题还有一种算法思路————动态规划。

f[i][x] 表示 i 分成 x 个非空的数的方案数。

显然 i<x 时 f[i][x]=0 , i=x 时 f[i][x]=1;

其余的状态，我们分情况讨论：

①有1的 ②没有1的

第一种情况，方案数为 f[i-1][x-1]

第二种情况，方案数为 f[i-x][x] (此时 i 必须大于 x)

所以，状态转移方程为： f[i][x]=f[i-1][x-1]+f[i-x][x]

程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;

int main() {
    int n, k;
    cin >> n >> k;
    int f[201][7]; // f[k][x] k 分成 x 份 ={f[k-1][x-1],f[k-x][x]}
    
    // 初始化边界条件
    for (int i = 1; i <= n; i++) {
        f[i][1] = 1;
        f[i][0] = 1;
    }
    for (int x = 2; x <= k; x++) {
        f[1][x] = 0;
        f[0][x] = 0;
    }

    // 动态规划求解
    for (int i = 2; i <= n; i++) {
        for (int x = 2; x <= k; x++) {
            if (i > x) {
                f[i][x] = f[i - 1][x - 1] + f[i - x][x];
            } else {
                f[i][x] = f[i - 1][x - 1];
            }
        }
    }
    
    // 输出结果
    cout << f[n][k];
    
    return 0;
}

奇怪的电梯

题目背景

感谢 @yummy 提供的一些数据。

题目描述

呵呵，有一天我做了一个梦，梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯，而且第 $i$ 层楼（$1 \le i \le N$）上有一个数字 $K_i$（$0 \le K_i \le N$）。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如： $3, 3, 1, 2, 5$ 代表了 $K_i$（$K_1=3$，$K_2=3$，……），从 $1$ 楼开始。在 $1$ 楼，按“上”可以到 $4$ 楼，按“下”是不起作用的，因为没有 $-2$ 楼。那么，从 $A$ 楼到 $B$ 楼至少要按几次按钮呢？

输入格式

共二行。

第一行为三个用空格隔开的正整数，表示 $N, A, B$（$1 \le N \le 200$，$1 \le A, B \le N$）。

第二行为 $N$ 个用空格隔开的非负整数，表示 $K_i$。

输出格式

一行，即最少按键次数，若无法到达，则输出 -1。

样例 #1

样例输入 #1

1
2
5 1 5
3 3 1 2 5

样例输出 #1

1
3

提示

对于 $100 %$ 的数据，$1 \le N \le 200$，$1 \le A, B \le N$，$0 \le K_i \le N$。

本题共 $16$ 个测试点，前 $15$ 个每个测试点 $6$ 分，最后一个测试点 $10$ 分。

这道题也可以多解，我们刚拿到题目的时候，肯定会直接思考模拟然后搜索，这题就可以用dfs或bfs来做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
int n,a,b,k[201],dis[201];
void dfs(int node,int step){
	dis[node]=step;//一定可以更新
	int v=node-k[node];
	if(1<=v&&step+1<dis[v]/*可以更新在搜索*/)//下
		dfs(v,step+1);
	v=node+k[node];
	if(v<=n&&step+1<dis[v])//上
		dfs(v,step+1);
	return;
}
int main(){
	memset(dis,0x3f,sizeof(dis));
	cin>>n>>a>>b;
	for(int i=1;i<=n;i++)
		cin>>k[i];
	dfs(a,0);
	cout<<(dis[b]==0x3f3f3f3f?-1:dis[b]);
	return 0;
}

注: 这个0x3f3f3f3f是个经验数字，他略小于int的最大值2^31-1的一半

这题第二个思路就是————最短路径

有没有很吃惊！我们可以把每一层楼抽象成图中的节点，然后构建邻接矩阵。然后随便写个Floyd算法就行了(因为本题的数据量比较小，而Floyd算法最简单，五行代码，可以用此方法大材小用)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<cstdio>
#define inf 99999999
using namespace std;
int main(){
	int n,a,b,t,i,j,k;
	int e[201][201];
	scanf("%d%d%d",&n,&a,&b);
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			if(i==j) e[i][j]=0;
			else e[i][j]=inf;
	for(int i=1;i<=n;i++){
		scanf("%d",&t);
		if(t+i<=n) e[i][t+i]=1;
		if(i-t>=1) e[i][i-t]=1;
	}
	for(k=1;k<=n;k++)
		for(i=1;i<=n;i++)	
			for(j=1;j<=n;j++)
				if(e[i][j]>e[i][k]+e[k][j])
					e[i][j]=e[i][k]+e[k][j];
	int ans=e[a][b];
	if(ans==inf) printf("-1");
	else printf("%d",ans);
	return 0;				
}

[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n-1$ 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$ ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1$ ， $2$ ， $9$ 。可以先将 $1$ 、 $2$ 堆合并，新堆数目为 $3$ ，耗费体力为 $3$ 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$ ，耗费体力为 $12$ 。所以多多总共耗费体力 $=3+12=15$ 。可以证明 $15$ 为最小的体力耗费值。

输入格式

共两行。
第一行是一个整数 $n(1\leq n\leq 10000)$ ，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i(1\leq a_i\leq 20000)$ 是第 $i$ 种果子的数目。

输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 $2^{31}$ 。

样例 #1

样例输入 #1

1
2
3 
1 2 9

样例输出 #1

1
15

提示

对于 $30%$ 的数据，保证有 $n \le 1000$：

对于 $50%$ 的数据，保证有 $n \le 5000$；

对于全部的数据，保证有 $n \le 10000$。

这题也有两种方法，总体都为贪心。

第一个方法其实就是上课天天讲的哈夫曼模版题，我这里没有直接使用C++的STL中的优先队列，手搓一个小根堆。时间复杂度为$O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<cstdio>
using namespace std;

int h[20010],n;
void swap(int x,int y){
	int t=h[x];
	h[x]=h[y];
	h[y]=t;
}
void siftdown(int i){
	int t,flag=0;
	while(i*2<=n && flag==0){
		if(h[i]>h[i*2])
			t=i*2;
		else
			t=i;
		if(i*2+1<=n)
			if(h[t]>h[i*2+1])
				t=i*2+1;
		if(t!=i){
			swap(t,i);
			i=t;
		}else
			flag=1;				
	}
	return ;
}
void creat(){
	for(int i=n/2;i>=1;i--)
		siftdown(i);
}
int main(){
	int num;
	scanf("%d",&num);
	//printf("ee\n");
	for(int i=1;i<=num;i++)
		scanf("%d",&h[i]);
	
	n=num;
	creat();       //建最小堆
	 
//	for(int i=1;i<=n;i++)
//		printf("%d ",h[i]);
//	printf("\n");
	
	int ans=0;
	
	for(int i=1;i<num;i++){
		ans+=h[1];
		if(n>=3 && h[3]<=h[2]){
				ans+=h[3];
				h[3]+=h[1];	
				siftdown(3);
			}
		else	
		if((n>=3 && h[2]<=h[3]) || n==2){
				ans+=h[2];
				h[2]+=h[1];	
				siftdown(2);
			}	
		h[1]=h[n--];
		siftdown(1);
//		for(int j=1;j<=n;j++)
//			printf("%d ",h[j]);
//		printf("\n");	
//		printf("ans=%d\n",ans);
	}
	
//	printf("sum=%d\n",sum);	
	printf("%d",ans);		
	return 0;
}

第二种方法是建立两个数组，第一个数组存储每堆果子的重量并从小往大排序。从第一个数组中取出前两个就是最小的两堆果子。把这两堆果子取出(从数组中划掉)合并一次成为新的一堆，记录消耗的体力，然后把这两堆果子的总和放在第二的数组后面。接下来还要用同样的方法找到最小的另一堆，合并，也放在第二个数组中，这两个数组都是从小往大排序的，所以两个数组中最小的那一堆一定就在两个数组没有被划掉的元素的最头部。重复这样的操作，直到最后两堆果子被合并。

这种算法时间复杂度还是O($nlogn$)，取决于排序的耗时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<cstring>
using namespace std;
#define maxn 20010
#define MAX 127
int main(){
	int n,a[maxn],b[maxn],m=0;
	scanf("%d",&n);
	memset(a,MAX,sizeof(a));
	memset(b,MAX,sizeof(b));
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	sort(a+1,a+n+1);
	// 注意a+1,a+n+1; 
	int i=1,j=1,ans=0;
	for(int k=1;k<n;k++){
		int w1=a[i]<b[j] ? a[i++] : b[j++];
		int w2=a[i]<b[j] ? a[i++] : b[j++];
//		printf("w1=%d\n",w1);
//		printf("w2=%d\n",w2);
		b[++m]=w1+w2;
		ans+=w1+w2;
	}	
	printf("%d",ans);
	return 0;
}

[NOIP1999 提高组] 导弹拦截

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

一行，若干个整数，中间由空格隔开。

输出格式

两行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例 #1

样例输入 #1

1
389 207 155 300 299 170 158 65

样例输出 #1

1
2
6
2

提示

对于前 $50%$ 数据（NOIP 原题数据），满足导弹的个数不超过 $10^4$ 个。该部分数据总分共 $100$ 分。可使用$\mathcal O(n^2)$ 做法通过。
对于后 $50%$ 的数据，满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。

对于全部数据，满足导弹的高度为正整数，且不超过 $5\times 10^4$。

此外本题开启 spj，每点两问，按问给分。

NOIP1999 提高组 第一题

$\text{upd 2022.8.24}$：新增加一组 Hack 数据。

1999年的经典老题。一个非升序列的dp加上贪心是可以解决的，大家都会做，本来是很简单的，但是后来加强了数据，这题的第一问dp还需要二分优化。

以下是个洛谷大佬的题解。

第一问

将拦截的导弹的高度提出来成为原高度序列的一个子序列，根据题意这个子序列中的元素是单调不增的（即后一项总是不大于前一项），我们称为单调不升子序列。本问所求能拦截到的最多的导弹，即求最长的单调不升子序列。

考虑记 $dp_{i}$ 表示「对于前 $i$ 个数，在选择第 $i$ 个数的情况下，得到的单调不升子序列的长度最长是多少」。于是可以分两种情况：

  • 第 $i$ 个数是子序列的第一项。则 $\mathit{dp}_i\gets 1$。
  • 第 $i$ 个数不是子序列的第一项。选择的第 $i$ 个数之前选择了第 $j$ 个数。根据题意，第 $j$ 个数的值 $h(j)$ 应当小于第 $i$ 个数的值 $h(i)$。枚举这样的 $j$，可以得到状态转移方程：

$$\mathit{dp}i=\max{j<i,h(j)\ge h(i)} {\mathit{dp_j}+1}$$

综合这两种情况，得到最终的状态转移方程：

$$\mathit{dp}i=\max{1,\max{j<i,h(j)\ge h(i)}{\mathit{dp}_j+1}}$$

值得注意的是，第 $n$ 个数不一定是最长单调不升子序列的最后一项。为了求出答案，我们需要枚举最后一项是哪个：

$$\mathit{ans}=\max_{1\le i\le n}{\mathit{dp}_i}$$

直接枚举进行状态转移，时间复杂度显然是 $ O(n^2)$。
下面考虑优化。

记 $f_i$ 表示「对于所有长度为 $i$ 的单调不升子序列，它的最后一项的大小」的最大值。特别地，若不存在则 $f_i=0$。下面证明：

  • 随 $i$ 增大，$f_i$ 单调不增。即 $f_i\ge f_{i+1}$。

考虑使用反证法。假设存在 $u<v$，满足 $f_u<f_v$。考虑长度为 $v$ 的单调不升子序列，根据定义它以 $f_v$ 结尾。显然我们可以从该序列中挑选出一个长度为 $u$ 的单调不升子序列，它的结尾同样是 $f_v$。那么由于 $f_v<f_u$，与 $f_u$ 最大相矛盾，得出矛盾。

因此 $f_i$ 应该是单调不增的。

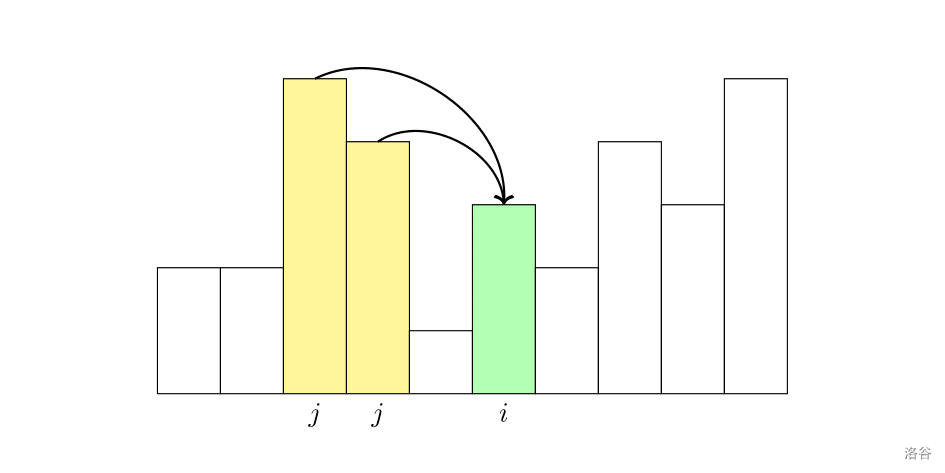
现在考虑以 $i$ 结尾的单调不升子序列的长度的最大值 $\mathit{dp}_i$。由于我们需要计算所有满足 $h(j)<h(i)$ 的 $j$ 中，$\mathit{dp}_j$ 的最大值，不妨考虑这个 $\mathit{dp}_j$ 的值是啥。设 $\mathit{dp}_j=x$，那么如果 $h(i)>f_x$，由于 $f_x\ge h(j)$，就有 $h(i)>h(j)$，矛盾，因此总有 $h(i)\le f_x$。

根据刚刚得出的结论，$f_i$ 单调不增，因此我们要找到尽可能大的 $x$ 满足 $h(i)\le f_x$。考虑二分。

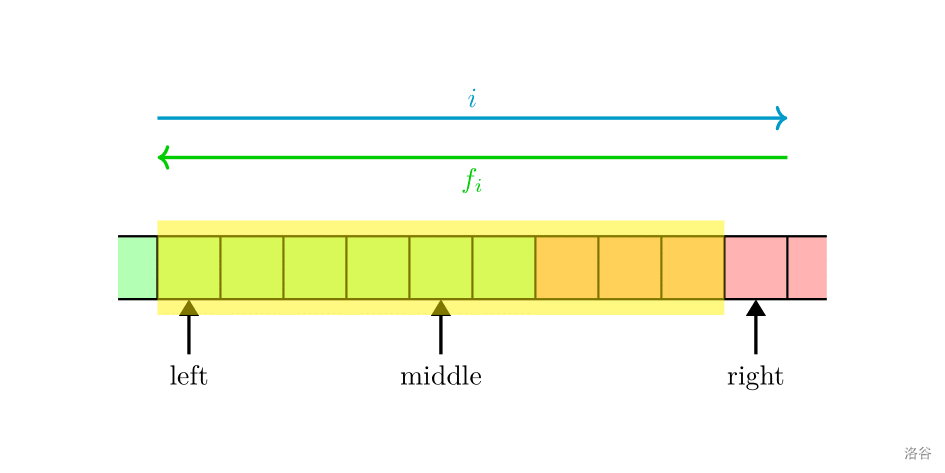
绿色区域表示合法的 $f_x$（即 $ f_x < h(i) $），红色区域表示不合法的 $f_x$（即 $f_x < h(i)$），我们需要找到红绿之间的交界点。

假设二分区域为 $[l,r)$（注意开闭区间。图上黄色区域标出来了二分区域内实际有效的元素）。每次取 $m=\frac{l+r}{2}$，如果 $f_m$ 在绿色区域内，我们就把 $l$ 移动到此处（$l\gets m$）；否则把 $r$ 移动到此处（$r\gets m$）。

当 $r-l=1$ 时，$l$ 处位置即为我们需要找的位置。转移 $\mathit{dp}i\gets l+1$ 即可。记得更新 $f$。但是我们只用更新 $f{\mathit{dp}i}$，这是因为 $f_1,f_2,\cdots f{\mathit{dp_i}-1}$ 的大小肯定都是不小于 $h(i)$ 的。$f_{\mathit{dp}i}$ 是最后一个不小于 $h(i)$ 的位置，$f{\mathit{dp}_i+1}$ 则小于 $h(i)$。

时间复杂度 $ O(nlogn)$，可以通过该问。

第二问

考虑贪心。

从左到右依次枚举每个导弹。假设现在有若干个导弹拦截系统可以拦截它，那么我们肯定选择这些系统当中位置最低的那一个。如果不存在任何一个导弹拦截系统可以拦截它，那我们只能新加一个系统了。

假设枚举到第 $i$ 个导弹时，有 $m$ 个系统。我们把这些系统的高度按照从小到大排列，依次记为 $g_1,g_2,\cdots g_m$。容易发现我们就是要找到最小的 $g_x$ 满足 $g_x\ge h_i$（与第一问相同，这是可以二分得到的），然后更新 $g_x$ 的值。更新之后，$g_1,g_2\cdots g_x$ 显然还是单调不增的，因此不用重新排序；如果找不到符合要求的导弹拦截系统，那就说明 $g_m < h_i$，直接在后头增加一个就行。

时间复杂度 $ O(nlogn)$，可以通过该问。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include&lt;bits/stdc++.h&gt;
#define up(l,r,i) for(int i=l,END##i=r;i&lt;=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i&gt;=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e5+3;
int n,t,H[MAXN],F[MAXN];
int main(){
    while(~scanf(&quot;%d&quot;,&amp;H[++n])); --n;
    t=0,memset(F,0,sizeof(F)),F[0]=INF;
    up(1,n,i){
        int l=0,r=t+1; while(r-l&gt;1){
            int m=l+(r-l)/2;
            if(F[m]&gt;=H[i]) l=m; else r=m;
        }
        int x=l+1;  // dp[i]
        if(x&gt;t) t=x; F[x]=H[i];
    }
    printf(&quot;%d\n&quot;,t);
    t=0,memset(F,0,sizeof(F)),F[0]=0;
    up(1,n,i){
        int l=0,r=t+1; while(r-l&gt;1){
            int m=l+(r-l)/2;
            if(F[m]&lt;H[i]) l=m; else r=m;
        }
        int x=l+1;
        if(x&gt;t) t=x; F[x]=H[i];
    }
    printf(&quot;%d\n&quot;,t);
    return 0;
}

观察第二问的代码，与第一问进行比较，可以发现这段代码等价于计算最长上升子序列（严格上升，即后一项大于前一项）。这其实是 $\text{Dilworth}$ 定理（将一个序列剖成若干个单调不升子序列的最小个数等于该序列最长上升子序列的个数），本处从代码角度证明了该结论。

[NOIP2003 普及组] 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

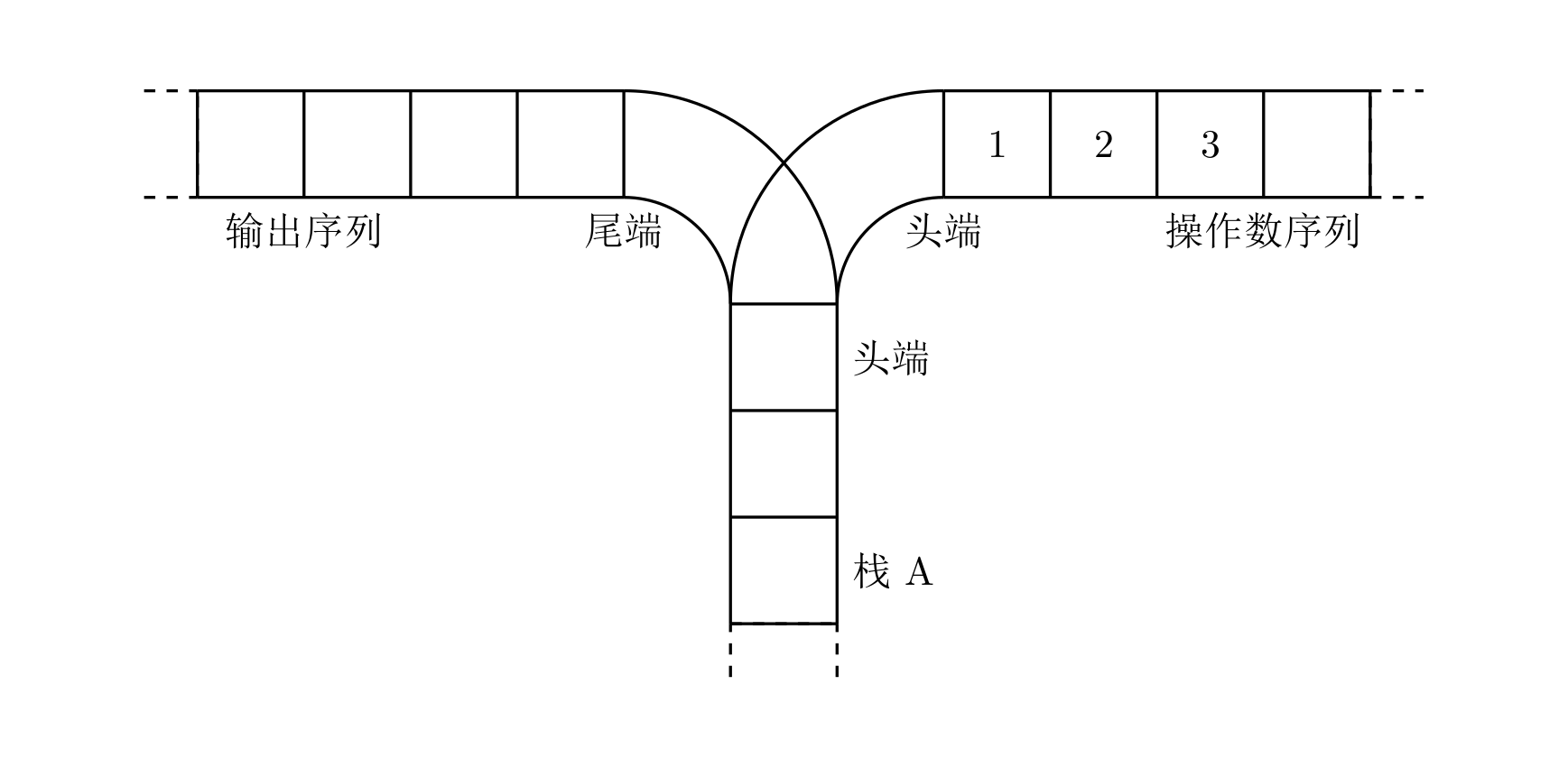
宁宁考虑的是这样一个问题：一个操作数序列，$1,2,\ldots ,n$（图示为 1 到 3 的情况），栈 A 的深度大于 $n$。

现在可以进行两种操作，

  1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
  2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

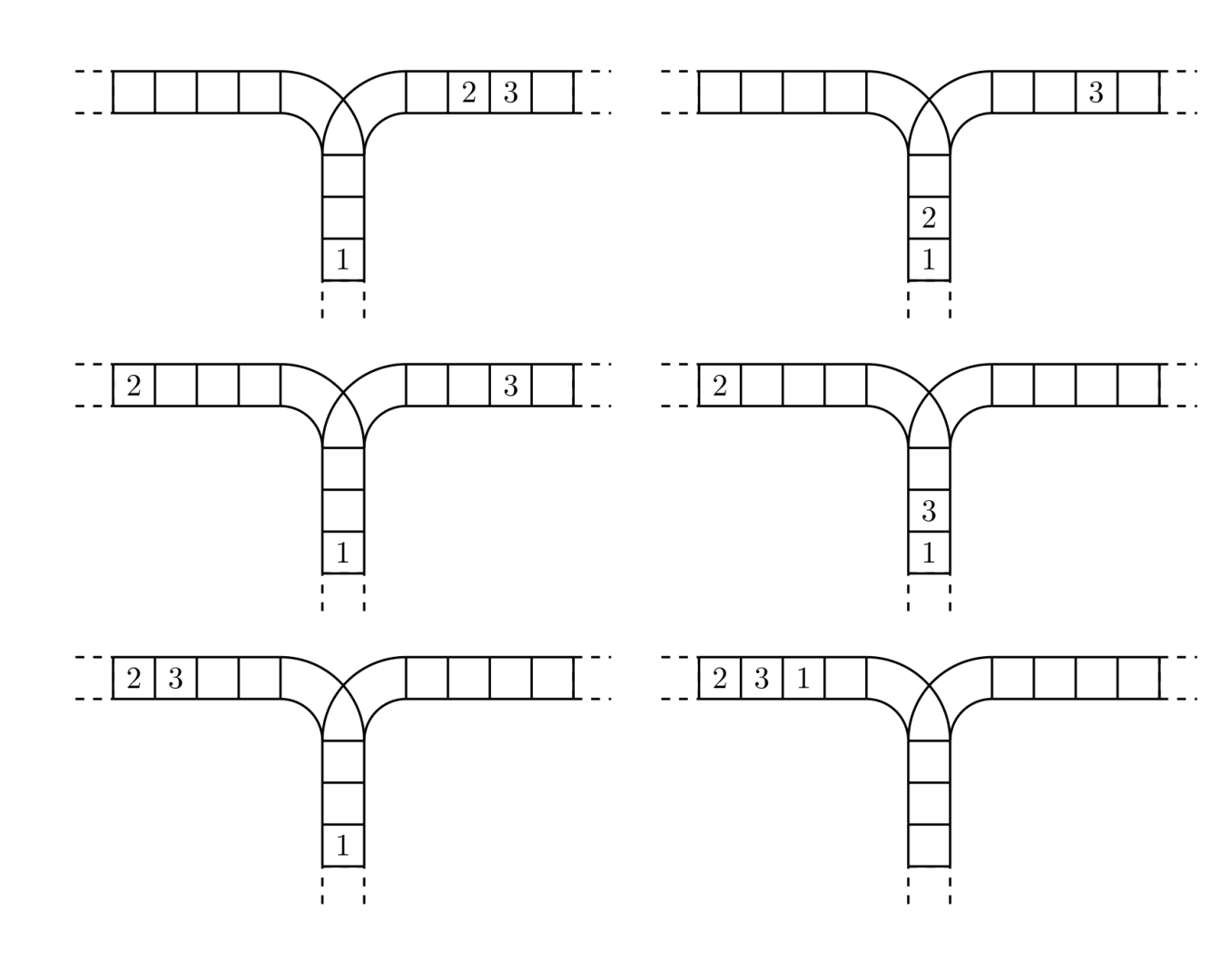
（原始状态如上图所示）

你的程序将对给定的 $n$，计算并输出由操作数序列 $1,2,\ldots,n$ 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 $n$（$1 \leq n \leq 18$）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例 #1

样例输入 #1

1
3

样例输出 #1

1
5

提示

【题目来源】

NOIP 2003 普及组第三题

这道题关于一个上课时老师提了一嘴的Catalan(卡特兰数)。这道题要动手动笔，找到数的规律。

我们只要顺着递归的思路来就好了：

  1. 据上面的递归，可知定义的 $f[i,j]$ 中 $i=0$ 时这个数组的值都为1，同时，这也是递推边界。并且，我们用 $i$ 表示队列里的数，$j$ 表示出栈数，$f[i,j]$表示情况数；
  2. 既然我们愉快地得到了递推思路，愣着干嘛，因为即使初始化了我们也不可能直接用递归的思路写出递归！所以开始找规律：$f[i,j]$到底与什么有着不可告人的联系？其实这个很容易可以想到：当 $i$ 个数进栈，$j-1$ 个数出栈的时候，只要再出一个数，便是i个数进栈，$j$ 个数出栈的情况，同理，对于进栈 $i-1$ 个数，出栈 $j$个数，在进栈一个数便是$f[i,j]$了，于是就有了递归式：$f[i,j]=f[i-1,j+1]$.
  3. 然而事实上这还没有完，因为 $i=j$ 时，栈空了，那么，此时就必须进栈了，则$i-1$，有$f[i,j]=f[i-1,j]$；解释一下为什么这样会栈空：当队列和出栈的数都有i个数时，数的总数为 $2i$ ，很明显的，栈里面没有元素了！
  • 递推式：

$f[n]=f[0]*f[n-1] + f[1]*f[n-2] + … + f[n-1]*f[0] (n≥2)$

完整代码就只有这么长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<cstdio>
#include<cstring>
using namespace std;
int main(){
	int n, h[20];
	memset(h,0,sizeof(h));
	h[0]=h[1]=1;
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
		for(int j=0;j<i;j++)
			h[i]+=h[j]*h[i-j-1];
	printf("%d",h[n]);		 
	return 0;
}

[NOIP2010 提高组] 关押罪犯

题目背景

NOIP2010 提高组 T3

题目描述

S 城现有两座监狱，一共关押着 $N$ 名罪犯，编号分别为 $1\sim N$。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 $c$ 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 $c$ 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 $N$ 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式

每行中两个数之间用一个空格隔开。第一行为两个正整数 $N,M$，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 $M$ 行每行为三个正整数 $a_j,b_j,c_j$，表示 $a_j$ 号和 $b_j$ 号罪犯之间存在仇恨，其怨气值为 $c_j$。数据保证 $1<a_j\leq b_j\leq N, 0 < c_j\leq 10^9$，且每对罪犯组合只出现一次。

输出格式

共一行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

样例输出 #1

1
3512

提示

输入输出样例说明

罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是 $3512$（由 $2$ 号和 $3$ 号罪犯引发）。其他任何分法都不会比这个分法更优。

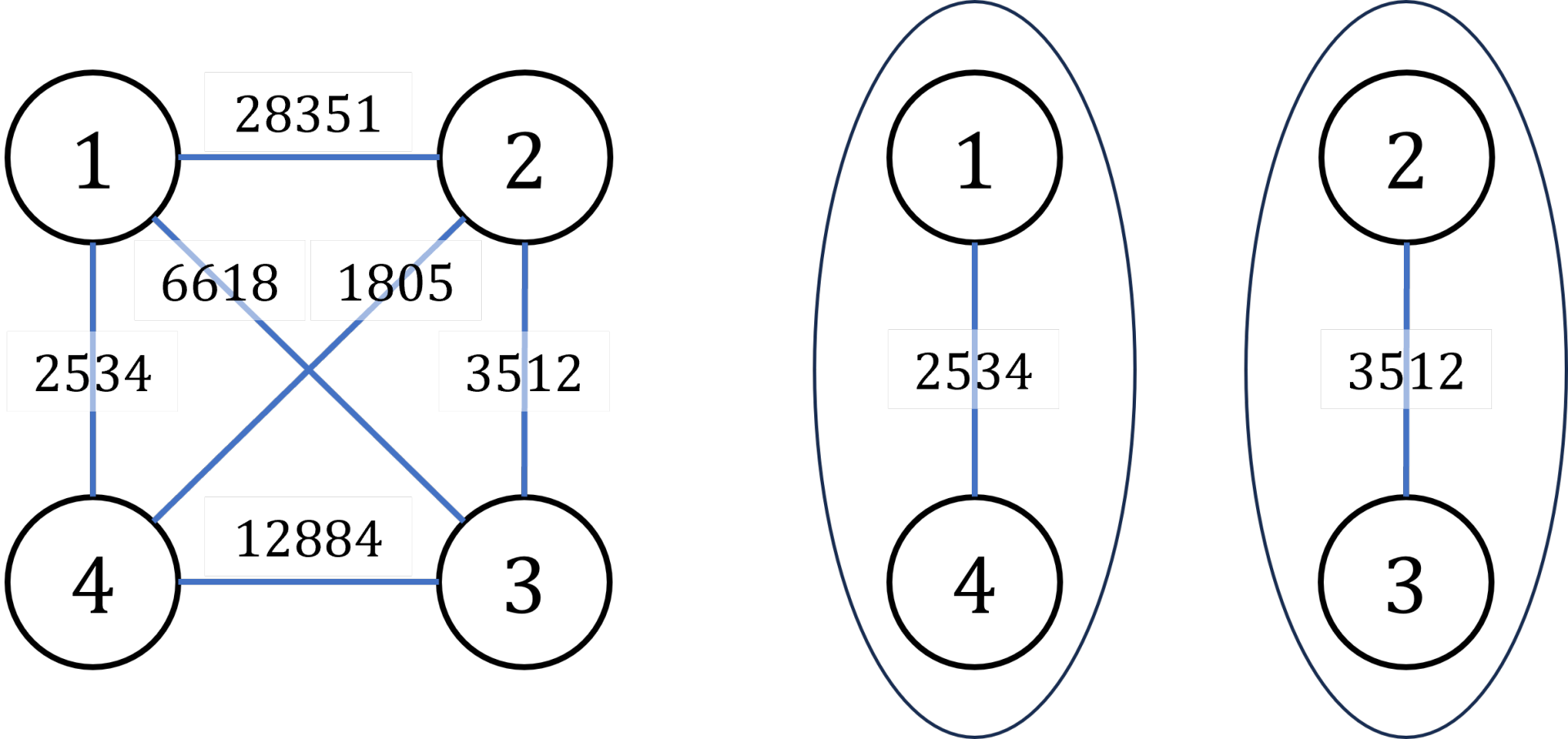
数据范围

对于 $30%$ 的数据有 $N\leq 15$。

对于 $70%$ 的数据有 $N\leq 2000,M\leq 50000$。

对于 $100%$ 的数据有 $N\leq 20000,M\leq 100000$。

这可能是我在这里放的知识难度最高的题目了，涉及种类并查集，虽然在洛谷中排行为一道绿题，但是只要各种并查集知识牢靠，想到思路还是挺容易。对，就是那种朋友的朋友是朋友，敌人的敌人是朋友。朋友的朋友还好处理，直接划在同一个集合就行了，但是敌人的敌人怎么处理呢？请看下面题解。

前言：

在数据结构并查集中，种类并查集属于扩展域并查集一类。

比较典型的题目就是：食物链（比本题难一些，有三个种类存在）

首先讲一下本题的贪心，这个是必须要懂的。我们假设最后Z 市长看到的那个冲突事件的影响力为 x （也就是有一对仇恨值为 x 的罪犯在同一监狱）那么比 x 仇恨值更高的每一对罪犯必须分配到不同的监狱（不然，最终答案就不是 x ，而是这一对罪犯的仇恨值了）；

所以本题是存在单调性的，只需要从大到小枚举仇恨值，到那一对与前面出现矛盾了，直接输出即可；

思路：

种类并查集中“种类”这个词也不是绝对的，它也可以说是一种关系，而本题的关系就在于要将罪犯分配到的两个监狱；我们可以将数组开到两倍来模拟这两个监狱（用A，B表示），每个罪犯在监狱中都有一个位置。

假设现在要把两个有仇的罪犯分别放到 A 或 B 中，我们发现如果要满足这一对的要求（即分到的监狱不同），那么如果第一个罪犯在 A 监狱，第二个罪犯必须在 B 监狱，反之也一样。

所以我们可以将 A 监狱中第一个罪犯的位置与 B 监狱中第二个罪犯的位置用并查集维护，即这样合并才能保证分到的监狱不一样。但第一个罪犯不一定只能在 A 监狱，所以我们将 B 监狱中 第一个罪犯的位置与 A 监狱中第二个罪犯的位置维护。

而出现矛盾的情况，举个例子： a 和 c 有仇，b 和 c 有仇，那么此时 a 和 c 在不同监狱，b 和 c 也在不同监狱，也就是说 a 和 b 一定在一个监狱。可一旦此时 a 和 b 有仇那么就矛盾了，因为a 和 b 要在不同监狱不然会有矛盾，可 a 和 b 已经在之前判定为必须在同一监狱，所会矛盾，此时就可以直接输出 a 和 b 的仇恨值（原理参见前言的贪心）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=20005;
const int MAXM=100005;
int f[2*MAXN]; // 开两倍数组
struct Relationship{
	int x,y,v;
}r[2*MAXM];
bool cmp(Relationship a,Relationship b){
	return a.v>b.v;
}
int find(int x){
	return x==f[x]?x:f[x]=find(f[x]);
}
void merge(int x,int y){
	int fx=find(x);
	int fy=find(y);
	if(fx != fy)
		f[fx]=fy;
}
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=2*n;i++)
		f[i]=i;
	for(int i=1;i<=m;i++)
		scanf("%d%d%d",&r[i].x,&r[i].y,&r[i].v);
	sort(r+1,r+m+1,cmp);
	for(int i=1;i<=m;i++){
		if(find(r[i].x)==find(r[i].y)){
			printf("%d",r[i].v);
			return 0;
		}
		else{
			merge(r[i].x+n,r[i].y);
			merge(r[i].y+n,r[i].x);
		}
	}	
	printf("0");
	return 0;
}

[USACO05FEB] Aggressive cows G

题目描述

农夫约翰建造了一座有 $n$ 间牛舍的小屋，牛舍排在一条直线上，第 $i$ 间牛舍在 $x_i$ 的位置，但是约翰的 $m$ 头牛对小屋很不满意，因此经常互相攻击。约翰为了防止牛之间互相伤害，因此决定把每头牛都放在离其它牛尽可能远的牛舍。也就是要最大化最近的两头牛之间的距离。

牛们并不喜欢这种布局，而且几头牛放在一个隔间里，它们就要发生争斗。为了不让牛互相伤害。约翰决定自己给牛分配隔间，使任意两头牛之间的最小距离尽可能的大，那么，这个最大的最小距离是多少呢？

输入格式

第一行用空格分隔的两个整数 $n$ 和 $m$；

第二行为 $n$ 个用空格隔开的整数，表示位置 $x_i$。

输出格式

一行一个整数，表示最大的最小距离值。

样例 #1

样例输入 #1

1
2
5 3
1 2 8 4 9

样例输出 #1

1
3

提示

把牛放在 $1$，$4$，$8$ 这三个位置，距离是 $3$。容易证明最小距离已经最大。

对于 $100%$ 的数据，$2 \le n \le 10^5$，$0 \le x_i \le 10^9$，$2 \le m \le n$。

不保证 $a$ 数组单调递增。

一个非常经典的二分答案例题，常常放在学校里市里的中小学NOIP选拔赛中。

一般我们根据经验看到什么指标最小的最大，最大的最小就可以判断这题就是一道二分答案题。

什么是二分答案？简单地说，就是和二分查找相似，二分每个答案，然后对这个答案进行求证，看是否满足条件，然后再次进行左右区间查找，直到二分到单个点上。

二分答案主要就是检验函数难写,check()本来就是二分答案的考察点。

对了，这题走来还要先排个序，直接上代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h> 
using namespace std;

#define INF 1e9
int a[100005],n,m;
bool check(int dis){
	int k=0,last=-INF;
	//k记录入住隔间的牛数量,last记录上一头牛的位置 
	for(int i=1;i<=n;i++)
		if(a[i]-last>=dis){//能安置就安置 
			last = a[i]; 
			k++;
		}
	return k>=m;
	//如果k>=m说明入住的牛多了，这个解ans小了，要向右查找	
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
		
	sort(a+1,a+n+1);//从小大快排 
	
	//二分答案的标准模版 
	int l=0,r=INF,ans,mid;
	while(l<=r){
		mid = (l + r)/2;
		if(check(mid)){
			ans=mid;
			l = mid + 1;
		}
		else
			r = mid - 1;
	}
	cout<<ans;
	return 0;
}

[NOIP2018 普及组] 龙虎斗

题目背景

NOIP2018 普及组 T2

题目描述

轩轩和凯凯正在玩一款叫《龙虎斗》的游戏，游戏的棋盘是一条线段，线段上有 $n$ 个兵营（自左至右编号 $1 \sim n$），相邻编号的兵营之间相隔 $1$ 厘米，即棋盘为长度为 $n-1$ 厘米的线段。$i$ 号兵营里有 $c_i$位工兵。 下面图 1 为 $n=6$ 的示例：

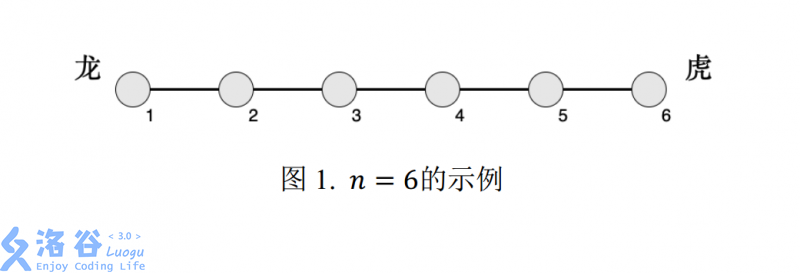
轩轩在左侧，代表“龙”；凯凯在右侧，代表“虎”。 他们以 $m$ 号兵营作为分界， 靠左的工兵属于龙势力，靠右的工兵属于虎势力，而第 $m$ 号兵营中的工兵很纠结，他们不属于任何一方。

一个兵营的气势为：该兵营中的工兵数$ \times $ 该兵营到 $m$ 号兵营的距离；参与游戏 一方的势力定义为：属于这一方所有兵营的气势之和。
下面图 2 为 $n = 6,m = 4$ 的示例，其中红色为龙方，黄色为虎方：

游戏过程中，某一刻天降神兵，共有 $s_1$ 位工兵突然出现在了 $p_1$ 号兵营。作为轩轩和凯凯的朋友，你知道如果龙虎双方气势差距太悬殊，轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续，你需要选择一个兵营 $p_2$，并将你手里的 $s_2$ 位工兵全部派往 兵营 $p_2$，使得双方气势差距尽可能小。

注意：你手中的工兵落在哪个兵营，就和该兵营中其他工兵有相同的势力归属（如果落在 $m$ 号兵营，则不属于任何势力）。

输入格式

输入文件的第一行包含一个正整数$n$，代表兵营的数量。

接下来的一行包含 $n$ 个正整数，相邻两数之间以一个空格分隔，第 $i$ 个正整数代 表编号为 $i$ 的兵营中起始时的工兵数量 $c_i$。

接下来的一行包含四个正整数，相邻两数间以一个空格分隔，分别代表 $m,p_1,s_1,s_2$。

输出格式

输出文件有一行，包含一个正整数，即 $p_2$，表示你选择的兵营编号。如果存在多个编号同时满足最优，取最小的编号。

样例 #1

样例输入 #1

1
2
3
6 
2 3 2 3 2 3 
4 6 5 2

样例输出 #1

1
2

样例 #2

样例输入 #2

1
2
3
6 
1 1 1 1 1 16 
5 4 1 1

样例输出 #2

1
1

提示

样例 1 说明

见问题描述中的图 2。
双方以 $m=4$ 号兵营分界，有 $s_1=5$ 位工兵突然出现在 $p_1=6$ 号兵营。
龙方的气势为：
$$2 \times (4-1)+3 \times (4-2)+2 \times (4-3) = 14$$
虎方的气势为：
$$2 \times (5 - 4) + (3 + 5) \times (6 - 4) = 18$$
当你将手中的 $s_2 = 2$ 位工兵派往 $p_2 = 2$ 号兵营时，龙方的气势变为：
$$14 + 2 \times (4 - 2) = 18$$
此时双方气势相等。

样例 2 说明

双方以 $m = 5$ 号兵营分界，有 $s_1 = 1$ 位工兵突然出现在 $p_1 = 4$ 号兵营。
龙方的气势为：
$$1 \times (5 - 1) + 1 \times (5 - 2) + 1 \times (5 - 3) + (1 + 1) \times (5 - 4) = 11$$
虎方的气势为：
$$16 \times (6 - 5) = 16$$
当你将手中的 $s_2 = 1$ 位工兵派往 $p_2 = 1$ 号兵营时，龙方的气势变为：
$$11 + 1 \times (5 - 1) = 15$$
此时可以使双方气势的差距最小。

数据规模与约定

$1 < m < n,1 ≤ p_1 ≤ n$。
对于 $20%$ 的数据，$n = 3,m = 2, c_i = 1, s_1,s_2 ≤ 100$。
另有 $20%$ 的数据，$n ≤ 10, p_1 = m, c_i = 1, s_1,s_2 ≤ 100$。
对于 $60%$ 的数据，$n ≤ 100, c_i = 1, s_1,s_2 ≤ 100$。
对于 $80%$ 的数据，$n ≤ 100, c_i,s_1,s_2 ≤ 100$。
对于 $100%$ 的数据，$n≤10^5$,$c_i,s_1,s_2≤10^9$。

最后，为什么要放这道题呢，这道题其实是我当年初二时OI的考试题，我非常有印象，当时还压线考了个普及组一等，这道就是只有六十几分。

首先……这题我在考场上打了一个暴力

当时我觉得这题很简单，就是先输入，p1位置加s1个工兵，然后依次枚举把s2个工兵放在所有的兵营里，每次算一遍双方势力之差，取最小就行了

然而我万万没想到竟然超时了……

详见代码，接下来解释为什么超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <cstdio>

int m, p1, s1, s2, a[1000005];
int n;

int compute (int x) {//计算双方势力之差
    int sum1 = 0, sum2 = 0;//计算左边和右边
    a[x] += s2;//先假设位置x加上s2个工兵
    for(int i = 1; i <= n; i ++ ) {
        if(i == m) continue;//m号兵营跳过
        else if(i < m) sum1 += (m - i) * a[i];//m左边的兵营
        else sum2 += (i - m) * a[i];
    }
    a[x] -= s2;//再减去s2个，因为是假设加上了s2个工兵
    if(sum1 >= sum2) return sum1 - sum2; return sum2 - sum1;
}

int main () {
    
    int min = 2e8, where;
    
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ )
        scanf("%d", &a[i]);
    scanf("%d%d%d%d", &m, &p1, &s1, &s2);
    
    a[p1] += s1;//加上s1个工兵
    
    for(int i = 1; i <= n; i ++ ) {
        int tmp = compute(i);//算一下势力之差
        if(min > tmp) {//如果比之前的最小还小（因为如果势力之差一样小就取编号小的，所以没等号）
            min = tmp;
            where = i;
        }
    }
    
    printf("%d", where);
    
    return 0;
}

为什么超时了呢？原因在于每次都算了一遍势力之差。

时间复杂度是$O(n^2)$

啥？那咋办？

就提前算好龙方和虎方的势力之差，每次枚举的时候就直接算一下新的势力之差就行了

别着急，没完呢，别抄这个，因为也是错的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>

inline int abs (int x, int y) {//相减后再算绝对值
    if(x >= y) return x - y;
    return y - x;
}

int m, p1, s1, s2, a[1000005];
int n;

int main () {
    
    int min = 2e8, where;
    int sum1 = 0, sum2 = 0;//分别提前算好左边和右边的势力
    
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ ) {
        scanf("%d", &a[i]);
    }
    scanf("%d%d%d%d", &m, &p1, &s1, &s2);
    
    a[p1] += s1;
    
    for(int i = 1; i <= n; i ++ ) {
        if(i < m) sum1 += (m - i) * a[i];
        else if(i > m) sum2 += (i - m) * a[i];//这是预处理，算好左边和右边的势力之差
    }
    
    for(int i = 1; i <= n; i ++ ) {
        if(i < m) sum1 += (m - i) * s2;
        else if(i > m) sum2 += (i - m) * s2;//算出新的双方势力
        int tmp = abs(sum1, sum2);//相减后算绝对值
        if(min > tmp) {
            min = tmp;
            where = i;
        }
        if(i < m) sum1 -= (m - i) * s2;
        else if(i > m) sum2 -= (i - m) * s2;//退栈
    }
    
    printf("%d", where);
    
    return 0;
}

满怀激动地提交，结果，后五个点WA了。。。

问题出在哪里？

原因是没开$long$ $long$。。。

因为虽然一个数$int$存的下，但加起来可是会超过$int$的啊！

（估算了下，在$1e18$ ~ $9e18$之间，$long$ $long$刚好够）

可恶的CCFNOI，竟然卡你longlong

于是，开成$long$ $long$就过了。

十年OI一场空，不开longlong见祖宗

后记

本篇为洛谷题解前8篇。虽然我早早就退出OI的圈子，但是我仍然还会想起当年的刷题经历。最后祝大家天天AC，AK。

参考链接:

【关押罪犯】https://www.luogu.com.cn/article/9ur7i0xl

【[NOIP1999 普及组] 导弹拦截】https://www.luogu.com.cn/article/yc19s69p

【栈】https://www.luogu.com.cn/article/vj5wm9da

【进击的奶牛】https://www.luogu.com.cn/article/fys1hulp