tensorflow入门实例(线性分类器)

Uncategorized
1.5k words

前言

在参加机器学习面试时，面试官可能会要求你用Tensorflow从头开始实现一个线性分类器。这是一项非常简单的任务，可以用于考察求职这是否具有基本的机器学习背景。

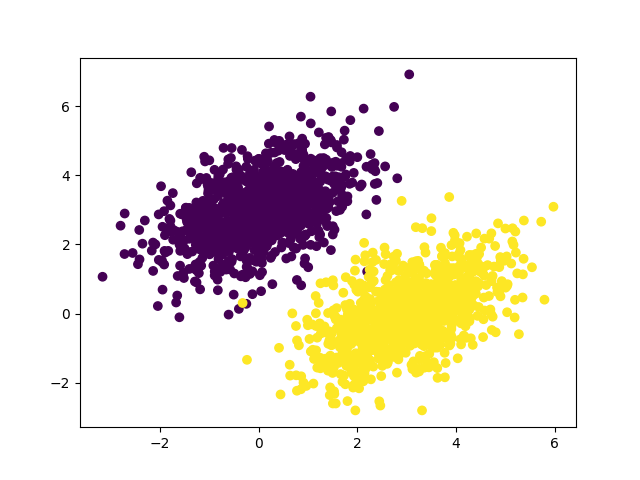
生成数据集

在二维平面上，生成两个类别线性可分的数据。生成办法是从一个具有特定协方差矩阵和特定均值的随机分布中抽取坐标来生成每一类点。

直观上讲，协方差矩阵描述了电云的形状，均值描述了电云的位置。

协方差矩阵在多维情况下用于描述多个随机变量之间的协方差关系。对于 n 个随机变量的情况，协方差矩阵是一个 n×n 的矩阵，其中第 i 行和第 j 列的元素表示第 i 个和第 j 个变量之间的协方差。

注意协方差矩阵是对称阵，对角线位置且都是1

createdots.py的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt

# 定义每个类别的样本数量，每个类别有1000个样本
num_samples_per_class = 1000 

# 负样本
negative_samples = np.random.multivariate_normal(
    mean= [0, 3],
    cov= [[1, 0.5],[0.5, 1]],
    size=num_samples_per_class
)

# 正样本
positive_samples = np.random.multivariate_normal(
    mean= [3, 0],
    cov= [[1, 0.5],[0.5, 1]],
    size=num_samples_per_class
)

# 输入数据集
inputs = np.vstack((negative_samples, positive_samples)).astype(np.float32)

# 目标(标签)数据集
targets = np.vstack((np.zeros((num_samples_per_class, 1), dtype="float32"), np.ones((num_samples_per_class, 1),dtype="float32")))

# 显示
plt.scatter(inputs[:, 0], inputs[:, 1], c=targets)
plt.show()

negative_samples = np.random.multivariate_normal(mean=[0, 3], cov=[[1, 0.5], [0.5, 1]], size=num_samples_per_class): 使用np.random.multivariate_normal函数生成一个二维高斯分布的负样本集合。mean参数指定了均值向量，cov参数指定了协方差矩阵，size参数指定生成样本的数量。这个函数生成了一个具有负标签的数据集，均值为[0, 3]，协方差矩阵为[[1, 0.5], [0.5, 1]]。

显示随机生成数据集

注意看在大概(0, 0)的位置有一个黄色点在紫色点的位置，在(2, 1)的周围也有个紫色点在黄色点的位置，过会再看这两个点0

训练模型

  1. 导入必要的库：

    • tensorflow 用于构建和训练神经网络模型。
    • matplotlib.pyplot 用于数据可视化。
    • numpy 用于数值计算。
    • createdots 是一个模块，用于导入名为 inputs 和 targets 的数据。

  2. 定义输入和输出维度：

    • input_dim = 2 表示输入数据的维度为2，这里是二维点。
    • output_dim = 1 表示模型的输出维度为1，即模型预测的每个样本的分数。

  3. 初始化模型参数：

    • w 和 b 是模型的权重和偏差，分别用 tf.Variable 初始化。w 是一个形状为 (input_dim, output_dim) 的矩阵，而 b 是一个形状为 (output_dim,) 的向量。

  4. 定义前向传播函数 model：

    • model(inputs) 通过矩阵乘法和偏差相加来计算模型的预测结果。

  5. 定义均方误差损失函数 square_loss：

    • square_loss(targets, predictions) 计算预测值与目标值之间的均方误差损失(MSE)。

  6. 设置学习率：

    • learning_rate = 0.1 表示训练过程中的学习率，用于控制参数更新的步长。

  7. 定义训练步骤函数 training_step：

    • 在这个函数中，使用 TensorFlow 的自动微分功能计算梯度，然后通过梯度下降法更新模型的参数 w 和 b，同时返回损失值。

  8. 进行训练：

    • 使用循环进行40次训练迭代，每次迭代调用 training_step 函数来更新模型参数，并打印出损失值。

  9. 预测：

    • 使用训练后的模型进行预测，将结果保存在 predictions 中。

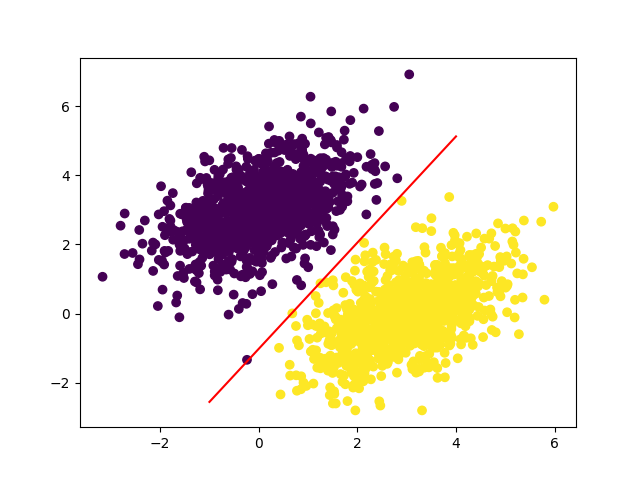
  10. 可视化显示分类结果：

    • 创建一个从 -1 到 4 的线性空间，计算模型的决策边界，然后使用 matplotlib.pyplot 绘制分类边界。
    • 使用 plt.scatter 绘制数据点，其中颜色表示预测结果是否大于0.5，用0.5作为分类的阈值。

model.py的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
from createdots import inputs, targets

# 输入的是二维点
input_dim = 2 

# 每个样本输出的预测值是一个分数(预测样本属于0，那么分数越接近0)
output_dim = 1

w = tf.Variable(initial_value=tf.random.uniform(shape=(input_dim, output_dim)))
b = tf.Variable(initial_value=tf.zeros(shape=(output_dim,)))

# 前向传播函数
def model(inputs):
    return tf.matmul(inputs, w) + b

# 均方误差损失函数
def square_loss(targets, predictions):
    per_sample_losses = tf.square(targets - predictions)
    return tf.reduce_mean(per_sample_losses)

# 学习率
learning_rate = 0.1  

# 训练步骤函数
def training_step(inputs, targets):
    with tf.GradientTape() as tape:
        predictions = model(inputs)
        loss = square_loss(targets, predictions)
    grad_loss_wrt_w, grad_loss_wrt_b = tape.gradient(loss, [w, b])
    w.assign_sub(grad_loss_wrt_w * learning_rate)
    b.assign_sub(grad_loss_wrt_b * learning_rate)
    return loss

# 训练40遍
for step in range(40):
    loss = training_step(inputs, targets)
    print(f"Loss at step {step}: {loss:.4f}")

# 预测
predictions = model(inputs)

# 可视化显示线性分类器
x = np.linspace(-1, 4, 100)
y = - w[0] / w[1] * x + (0.5 - b) / w[1]
plt.plot(x, y, "-r")
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5) # 用0.5这个阈值区分
plt.show()

仔细想想，prediction = [ [w1] , [w2] ] dot [x,y] +b = w1 * x + w2 * y + b, 又因为类别0是w1 * x + w2 * y +b < 0.5, 类别1是w1 * x + w2 * y +b > 0.5, 所以直线方程是w1 * x + w2 * y +b = 0.5，变形一下就是y = -w1/w2 * x + (0.5-b)/w2

训练结果，损失函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Loss at step 0: 2.8693
Loss at step 1: 0.4232
Loss at step 2: 0.1604
Loss at step 3: 0.1208
Loss at step 4: 0.1090
Loss at step 5: 0.1014
Loss at step 6: 0.0947
Loss at step 7: 0.0887
Loss at step 8: 0.0831
Loss at step 9: 0.0781 
Loss at step 10: 0.0735
Loss at step 11: 0.0693
Loss at step 12: 0.0654
Loss at step 13: 0.0619
Loss at step 14: 0.0587
Loss at step 15: 0.0557
Loss at step 16: 0.0530
Loss at step 17: 0.0506
Loss at step 18: 0.0483
Loss at step 19: 0.0462
Loss at step 20: 0.0444
Loss at step 21: 0.0426
Loss at step 22: 0.0411
Loss at step 23: 0.0396
Loss at step 24: 0.0383
Loss at step 25: 0.0371
Loss at step 26: 0.0360
Loss at step 27: 0.0350
Loss at step 28: 0.0341
Loss at step 29: 0.0332
Loss at step 30: 0.0325
Loss at step 31: 0.0318
Loss at step 32: 0.0311
Loss at step 33: 0.0305
Loss at step 34: 0.0300
Loss at step 35: 0.0295
Loss at step 36: 0.0291
Loss at step 37: 0.0286
Loss at step 38: 0.0283
Loss at step 39: 0.0279

现在斜线两边就全是紫点或黄点了。

参考：python深度学习