day6 - 走入新世界
动态规划(DP)
动态规划(Dynamic Programming)算法是解决多阶段决策过程最优的通用方法。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。
要了解动态规划的概念,首先要知道什么是多阶段决策问题。
多阶段决策问题
如果一类活动过程可以分为若干个互相联系的阶段,在每一个阶段都需作出决策(采取措施),一个阶段的决策确定以后,常常影响到下一个阶段的决策,从而就完全确定了一个过程的活动路线,则称它为多阶段决策问题。
各个阶段的决策构成一个决策序列,称为一个策略。每一个阶段都有若干个决策可供选择,因而就有许多策略供我们选取,对应于一个策略可以确定活动的效果,这个效果可以用数量来确定。策略不同,效果也不同,多阶段决策问题,就是要在可以选择的那些策略中间,选取一个最优策略,使在预定的标准下达到最好的效果。
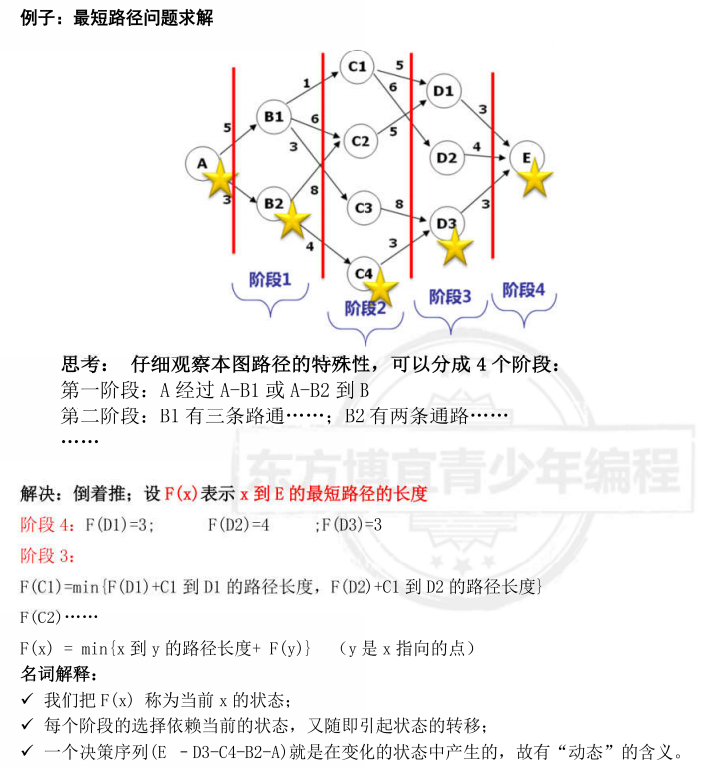
三个基本的概念:
- 阶段
问题的过程被分成若干相互联系的部分,我们成为阶段,以便按一定的次序求解。
- 状态
某一阶段的出发位置称为状态,通常一个阶段包含若干状态,如第3层有f(Cl)、f (C2)、 f(C3)、f(C4)状态。
- 决策
对问题的处理中作出的每种选择的行动就是决策。即从该阶段的每个状态出发,通过一次选择性的行动移至下一个阶段的相应状态。
举个栗子
还记的数塔问题吗?
解法一:复习一下dfs深度优先搜索
解法二:动态规划
加法具有交换律,考虑从下往上走,倒推。
动态规划状态转移方程:
dp[i, j] = a[i, j] + max{dp[i+1, j], dp[i+1, j+1]}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include<bits/stdc++.h>
using namespace std;
int main(){
int n,a[101][101];
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
cin>>a[i][j];
for(int i=n-1;i>=1;i--)
for(int j=1;j<=i;j++)
a[i][j]+=max(a[i+1][j],a[i+1][j+1]);
cout<<a[1][1];
return 0;
}
|
输入样例
输出
思考
- 贪心算法和动态规划的区别
局部最优?全局最优?背包问题?
分治算法和动态规划的区别
递推算法和动态规划的区别
跳楼梯算递推还是动规?它也有个算数公式。
- 习题:
洛谷P1002 [NOIP2002 普及组] 过河卒(必做)
说在前面做题要拿纸拿笔
思路:这题很简单,我只觉的是递推算法,不算动态规划。首先预处理一下,将不能走的区域dp[i][j]都置为0,其他的就是一个算式:
dp[i][j]=dp[i-1][j]+dp[i][j-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int main(){
int n,m,x,y,book[30][30];
long long dp[30][30];
memset(dp,0,sizeof(dp));
memset(book,0,sizeof(book));
cin>>n>>m>>x>>y;
n += 2;
m += 2;
x += 2;
y += 2;
book[x][y] = 1;
book[x+1][y-2] = 1;
book[x+1][y+2] = 1;
book[x-1][y-2] = 1;
book[x-1][y+2] = 1;
book[x+2][y-1] = 1;
book[x+2][y+1] = 1;
book[x-2][y-1] = 1;
book[x-2][y+1] = 1;
dp[2][2] = 1;
book[2][2] = 1;
for(int i=2;i<=n;i++)
for(int j=2;j<=m;j++)
if(book[i][j] == 0)
dp[i][j] = dp[i-1][j] + dp[i][j-1];
cout<<dp[n][m];
return 0;
}
|
做好觉悟了吗 —— 更多精彩的题目
洛谷题号B3637
最长上升子序列
题目描述
这是一个简单的动规板子题。
给出一个由 $n(n\le 5000)$ 个不超过 $10^6$ 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。
最长上升子序列是指,从原序列中按顺序取出一些数字排在一起,这些数字是逐渐增大的。
输入格式
第一行,一个整数 $n$,表示序列长度。
第二行有 $n$ 个整数,表示这个序列。
输出格式
一个整数表示答案。
样例 #1
样例输入 #1
样例输出 #1
提示
分别取出 $1$、$2$、$3$、$4$ 即可。
最长上升子序列,最长不下降子序列,最长下降子序列,最长不上升子序列,是一类这种问题。
动态转移方程:
dp[i]=1
dp[i]=max{dp[j]+1,dp[i]}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include<bits/stdc++.h>
using namespace std;
int main(){
int a[5005],dp[5005],n,ans=0;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++){
dp[i]=1;
for(int j=1;j<i;j++)
if(a[j]<a[i])
dp[i]=max(dp[i],dp[j]+1);
ans=max(ans,dp[i]);
}
cout<<ans;
return 0;
}
|
习题:P1020 [NOIP1999 普及组] 导弹拦截
贪心 + 动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include<stdio.h>
const int maxn=10010;
int max(int a,int b){
return a>b?a:b;
}
int main(){
int h[maxn],n=0,ans=0;
int f[maxn],hh[maxn],book[maxn];
while(scanf("%d",&h[n+1])==1){
n++;
f[n]=1;
book[n]=0;
}
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(h[j]<=h[i])
f[j]=max(f[j],f[i]+1);
for(int i=1;i<=n;i++)
ans=max(ans,f[i]);
printf("%d\n",ans);
ans=0;
for(int i=1;i<=n;i++)
if(book[i]==0){
book[i]=1;
int hmax=h[i];
ans++;
for(int j=i+1;j<=n;j++)
if(h[j]<=hmax && book[j]==0){
hmax=h[j];
book[j]=1;
}
}
printf("%d",ans);
return 0;
}
|
思考题:P1091 [NOIP2004 提高组] 合唱队形(选做,day6做不完就day7做)
提示:两个最长子序列在一起
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<cstdio>
#define maxn 110
using namespace std;
int max(int a,int b){
return a > b ? a : b;
}
int main(){
int n,t[maxn],dpa[maxn],dpb[maxn];
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&t[i]);
for(int i=1;i<=n;i++){
dpa[i]=1;
for(int j=1;j<i;j++)
if(t[j]<t[i])
dpa[i]=max(dpa[j]+1,dpa[i]);
}
for(int i=n;i>=1;i--){
dpb[i]=1;
for(int j=n;j>i;j--)
if(t[j]<t[i])
dpb[i]=max(dpb[j]+1,dpb[i]);
}
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,dpa[i]+dpb[i]-1);
printf("%d",n-ans);
return 0;
}
|

